B.L. Jan-99
Since the installation of dual-channel receivers (May, October 1998) at the 30-m telescope, frequency diplexing between the two channels of one dewar is accomplished via a Martin-Puplett interferometer (MPI). This document explains the essentials of the operation of such a diplexer.
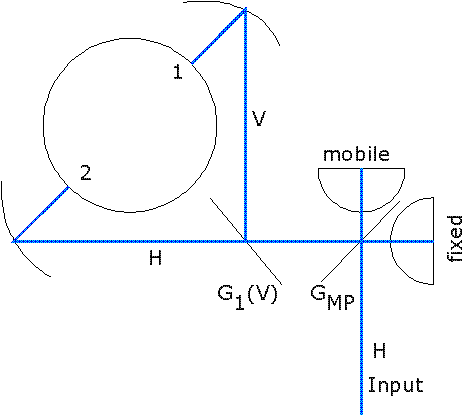
Each dual-channel receiver (i.e., each cryostat) is fed with a definite linear polarization. As far as the MPI diplexer is concerned, that input polarization can be assumed to be horizontal. Basically, the MPI grid GMP splits the incoming signal into two orthogonal components along axes at 45deg, and after bouncing from the fixed and mobile mirrors, the components are recombined with a variable path difference.

In general, the resulting polarization is elliptical. We do not need to enter the complexities of elliptical polarization, since the signal that emerges from the MPI is anlyzed by the vertical grid G1, which steers the signals, V-pol to channel 1, (Rx100 or Rx150), and H-pol to channel 2 (Rx230 or Rx270). So we need only consider the transmission from Input to 1 and 2 respectively, given by :
T1 = (1/2) [1 - cos(2*pi*delta*nu1/c)]
T2 = (1/2) [1 +cos(2*pi*delta*nu2/c)]
where delta is the path difference (twice the travel of the mobile mirror).
Accordingly, the losses are respectively :
L1 = (1/2) [1 +cos(2*pi*delta*nu1/c)]
L2 = (1/2) [1 - cos(2*pi*delta*nu2/c)]
We try to find a "fair" compromise between the two channels, i.e. to realize Lmin = min(max(L1,L2)), via a suitable algorithm.
The path difference delta can be many wavelengths (max 55mm in the current implementation). So, loosely speaking, one can hope that out of the many oscillations of L1 and L2 versus delta for a given pair of frequencies, one can find a value of delta that gives low values for both L1 and L2. The outcome depends on the ratio R = nu2/nu1.
The distinction between these classes is blurred somewhat by the finite range of values for delta.
The worst "Evil" values are 3:1 and 5:2, for which Lmin is respectively, 0.148 and 0.051. They can occur, e.g. for HCN(1-0)/(3-2) (outside the nominal freq range!) or CS(2-1)/(5-4). So try to stay away from these ratio, if possible by re-distributing the observed lines between receivers.
Real observations occur over a finite bandwidth. So, the optimization takes into account the average loss over a finite bandwidth, resp. B1 and B2. The loss equations are modified :
L1 = (1/2) [1 +(c/pi*delta*B1) * sin(pi*delta*B1/c) * cos(2*pi*delta*nu1/c)]
L2 = (1/2) [1 -(c/pi*delta*B2) * sin(pi*delta*B2/c) * cos(2*pi*delta*nu2/c)]
Each receiver has a small, but non-zero response in the image sideband. The losses of the diplexer at the image frequency, weighted by the image band gain, must be added to those in the signal sideband.
A finite set of values of delta is determined that give equal (but not necessarily small) values for the losses L1 and L2 at the spot frequencies nu1 and nu2. They are scanned and for each one the actual losses L1 and L2 are computed, taking into account finite bandwidth and rejection. The rejections are fixed at "typical" values, of resp. :
Two options are available for the bandwidth (the values are not critical) :
A MPI simulator is available to compute
the optimized losses for a pair of frequencies.
An observing Time
Estimator is also available, that gives a global estimate of observing
efficiency.
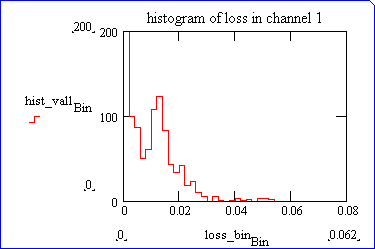
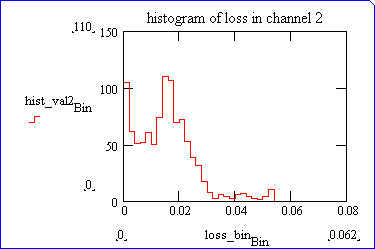
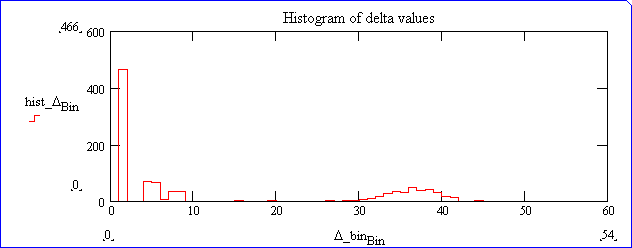
1024 pairs of frequencies have been randomly drawn from uniform distributions in the ranges [83-115] and [200-260], respectively for nu1 and nu2. The optimized losses have been computed for each pair, and the following histograms were produced. L1 is below 0.02 in 90% of cases, and L2 less than 0.025 in 90% of cases.