


Next: 10.4.1 Correction for the
Up: 10. Amplitude and Flux
Previous: 10.3.5 The program FLUX
10.4 Interferometric Calibration of the Amplitude
For antenna i, the antenna-based amplitude correction is given by (Eq.10.3
and 10.4).
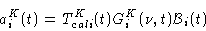 |
(10.14) |
where K = U or L. The decorrelation factor f (see R.Lucas lecture 7)
is not taken into account here because it is fundamentally a baseline-based
parameter.
In a baseline-based decomposition, the complex gain of baseline ij,
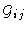 is
given by:
is
given by:
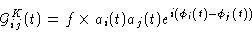 |
(10.15) |
and the amplitude of the baseline ij is
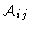
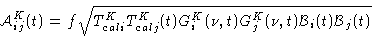 |
(10.16) |
We will discuss first the term
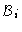 and estimate then the decorrelation factor
f, before giving a global scheme of the amplitude calibration.
and estimate then the decorrelation factor
f, before giving a global scheme of the amplitude calibration.



Next: 10.4.1 Correction for the
Up: 10. Amplitude and Flux
Previous: 10.3.5 The program FLUX
S.Guilloteau
2000-01-19
![]() is
given by:
is
given by: