



Next: 14.4.3 Regularization frequency list
Up: 14.4 Image reconstruction process
Previous: 14.4.1 Synthesized aperture
The neat beam can be regarded as a sort of optimal
clean beam: the optimal apodized point-spread function
that can be designed within the limits of the Heisenberg
principle. More precisely, the neat beam 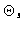 is a
centro-symmetric function lying in the object
space Ho, and satisfying the following properties:
is a
centro-symmetric function lying in the object
space Ho, and satisfying the following properties:
- The energy of
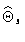 is concentrated in
is concentrated in
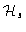 .
In other words,
.
In other words,
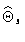 has to be small outside
has to be small outside
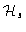 in the mean-square sense: we impose the fraction
in the mean-square sense: we impose the fraction 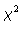 of this energy
in
of this energy
in
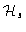 to be close to 1 (say
to be close to 1 (say
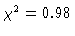 ).
).
- The effective support
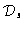 of
of 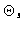 in Ho is as small
as possible with respect to the choice of
in Ho is as small
as possible with respect to the choice of
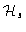 and
and 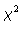 .
The idea is of course to have the best possible
resolution.
.
The idea is of course to have the best possible
resolution.
This apodized point-spread function is thus computed on the grounds
of a trade-off between resolution and efficiency, with the aid of the
power method.
Figure:
Experimental frequency coverage and
frequency coverage to be synthesized
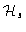 (left hand). The experimental frequency list
(left hand). The experimental frequency list
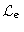 includes Ne=2862 frequency points. The
frequency coverage to be synthesized
includes Ne=2862 frequency points. The
frequency coverage to be synthesized
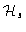 is centred in the Fourier grid
is centred in the Fourier grid
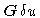 ,
where
,
where
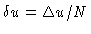 with N=128 (here, the diameter of
the circle is equal to
with N=128 (here, the diameter of
the circle is equal to
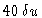 ).
The neat beam
).
The neat beam 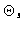 (right hand) represented here
corresponds to the frequency coverage to be synthesized
(right hand) represented here
corresponds to the frequency coverage to be synthesized
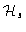 for a given value of
for a given value of
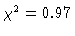 .
It is centred
in the object grid
.
It is centred
in the object grid
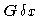 where
where
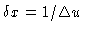 (here, the full width of
(here, the full width of  at half maximum is equal
to
at half maximum is equal
to
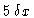 ).
).
![\begin{picture}(130,59)(0,0)
% width/height=435pt/400pt -> 63mm/58mm
\put(0,0){\...
...idth=60mm]{eafig4b.eps} }
\put(37,34){{\small$\mathcal{H}_s$ }}
%%
\end{picture}](img1061.gif) |




Next: 14.4.3 Regularization frequency list
Up: 14.4 Image reconstruction process
Previous: 14.4.1 Synthesized aperture
S.Guilloteau
2000-01-19
![\begin{picture}(130,59)(0,0)
% width/height=435pt/400pt -> 63mm/58mm
\put(0,0){\...
...idth=60mm]{eafig4b.eps} }
\put(37,34){{\small$\mathcal{H}_s$ }}
%%
\end{picture}](img1061.gif)