



Next: 14.4.5 Object representation space
Up: 14.4 Image reconstruction process
Previous: 14.4.3 Regularization frequency list
According to the definition of the image to be reconstructed, the
Fourier data corresponding to
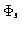 are defined by the relationship:
are defined by the relationship:
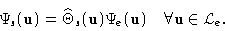 |
(14.9) |
Clearly,
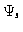 lies in the experimental data space Ke.
lies in the experimental data space Ke.
Let us now introduce the data vector:
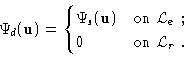 |
(14.10) |
This vector lies in the data space Kd, the real Euclidian space
underlying the space of complex-valued functions 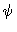 on
on
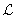 ,
such that
,
such that
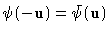 .
This space is equipped with the scalar product:
.
This space is equipped with the scalar product:
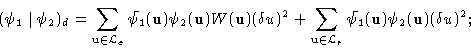 |
(14.11) |
W(u) is a given weighting function that
takes into account the reliability of the data via the standard
deviation
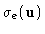 of
of
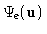 , as well
as the local redundancy
, as well
as the local redundancy
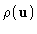 of
u up to
the sampling interval
of
u up to
the sampling interval 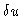 .
.
The Fourier sampling operator A is the operator from
the object space Ho into the data space Kd:
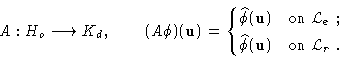 |
(14.12) |
As the experimental data
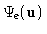 are blurred values
of
are blurred values
of
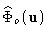 on
on
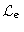 , this operator will
play a key role in the image reconstruction process. The definition of
this Fourier sampling operator suggests that the action of Ashould be decomposed into two components: Ae on the experimental
frequency list
, this operator will
play a key role in the image reconstruction process. The definition of
this Fourier sampling operator suggests that the action of Ashould be decomposed into two components: Ae on the experimental
frequency list
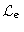 , and Ar on the regularization
frequency list
, and Ar on the regularization
frequency list
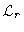 .
.




Next: 14.4.5 Object representation space
Up: 14.4 Image reconstruction process
Previous: 14.4.3 Regularization frequency list
S.Guilloteau
2000-01-19