next up previous contents
Next: 5.1.4 Signal phase Up: 5.1 An Heterodyne Interferometer Previous: 5.1.2 The heterodyne interferometer

5.1.3 Frequency conversion

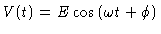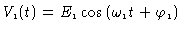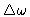The input signal to the mixer is $V(t) = E \cos{(\omega t + \phi)}$, and the first LO signal is $\ensuremath{V_\mathrm{\scriptscriptstyle 1}} (t) = \ensuremath{E_\mathrm{\scrip... ...criptscriptstyle 1}} t + \ensuremath{\varphi_\mathrm{\scriptscriptstyle 1}} )}$. Mixer output is proportional to $[V(t)+\ensuremath{V_\mathrm{\scriptscriptstyle 1}} (t)]^2$ and we select by a filter a band $\Delta \omega$ centered on 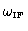\ensuremath{\omega_\mathrm{\scriptscriptstyle IF}}. 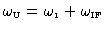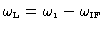We note: $\ensuremath{\omega_\mathrm{\scriptscriptstyle U}} = \ensuremath{\omega_\mathrm{\scriptscriptstyle 1}} + \ensuremath{\omega_\mathrm{\scriptscriptstyle IF}} $, and $\ensuremath{\omega_\mathrm{\scriptscriptstyle L}} = \ensuremath{\omega_\mathrm{\scriptscriptstyle 1}} - \ensuremath{\omega_\mathrm{\scriptscriptstyle IF}} $ the angular frequencies in the upper side band and in the lower side band, respectively.
The IF output is
$\displaystyle \ensuremath{V_\mathrm{\scriptscriptstyle IF}} (t)$ $\textstyle \propto$ $\displaystyle \ensuremath{E_\mathrm{\scriptscriptstyle U}}\cos{[(\ensuremath{\o... ...m{\scriptscriptstyle L}} +\ensuremath{\varphi_\mathrm{\scriptscriptstyle 1}} ]}$  
$\displaystyle \ensuremath{V_\mathrm{\scriptscriptstyle IF}} (t)$ $\textstyle \propto$ $\displaystyle \ensuremath{E_\mathrm{\scriptscriptstyle U}}\cos{(\ensuremath{\om... ...m{\scriptscriptstyle L}} +\ensuremath{\varphi_\mathrm{\scriptscriptstyle 1}} )}$ (5.2)

After the frequency conversion the phase is the difference of the signal phase ant the LO phase, with a sign reversal if the conversion is lower side band:
  USB LSB
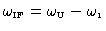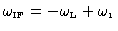frequency: $\ensuremath{\omega_\mathrm{\scriptscriptstyle IF}} =\ensuremath{\omega_\mathrm{\scriptscriptstyle U}} -\ensuremath{\omega_\mathrm{\scriptscriptstyle 1}} $ $\ensuremath{\omega_\mathrm{\scriptscriptstyle IF}} =-\ensuremath{\omega_\mathrm{\scriptscriptstyle L}} +\ensuremath{\omega_\mathrm{\scriptscriptstyle 1}} $
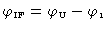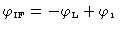phase: $\ensuremath{\varphi_\mathrm{\scriptscriptstyle IF}} = \ensuremath{\varphi_\mathrm{\scriptscriptstyle U}} -\ensuremath{\varphi_\mathrm{\scriptscriptstyle 1}} $ $\ensuremath{\varphi_\mathrm{\scriptscriptstyle IF}} =-\ensuremath{\varphi_\mathrm{\scriptscriptstyle L}} +\ensuremath{\varphi_\mathrm{\scriptscriptstyle 1}} $

next up previous contents
Next: 5.1.4 Signal phase Up: 5.1 An Heterodyne Interferometer Previous: 5.1.2 The heterodyne interferometer
S.Guilloteau
2000-01-19