



Next: 7.1.2 Gain corrections
Up: 7.1 Definitions and formalism
Previous: 7.1 Definitions and formalism
Since amplitude and phase distortions have different physical origins it is
generally useful to write
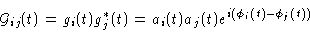 |
(7.2) |
Here we have split the gains into antenna based factors. This is
generally legitimate since the gains represent properties of the
data acquisition chains which are in the analogue part of the
system. The correlator itself is a digital machine and we assume it
is perfectly working (including the clipping correction). This
assumption is certainly valid when considering a single frequency
and a single instant. When we start averaging in time or frequency,
the average of the product may not be the product of averages, and
we may have some baseline-based effects.
The baseline-based gains can be determined by observing a point
source. This is usually a strong quasar. In that case the true
visibilities
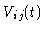 should all be equal to the quasar flux
density S. Then
should all be equal to the quasar flux
density S. Then
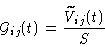 |
(7.3) |
The antenna gains gi(t) can also be deduced from the non-linear set of
equations:
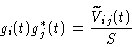 |
(7.4) |
This is a system with N complex unknowns and N (N-1)/2 equations.
In terms of real quantities there are N (N-1) measured values
(amplitudes and phases; there are only 2 N-1 unknowns since one
may add a phase factor to all complex gains without affecting the
baseline-based complex gains. When N is larger than 2 the system
is over determined and may be solved by a method of least squares.
If we note
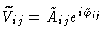 ,
the equations for phases are simply:
,
the equations for phases are simply:
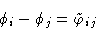 |
(7.5) |
It can be shown that the least-squares solutions (when the same weight
is given to all baselines, and if we impose the condition
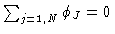 ), is given by:
), is given by:
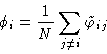 |
(7.6) |
For the amplitudes we can define in order to get a linear system:
This time the least square solution is, when the same weight
is given to all baselines:
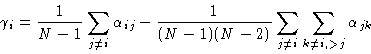 |
(7.9) |
Obviously this antenna gain determination needs at least three antennas.
For three antennas it reduces to the obvious result:
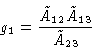 |
(7.10) |
These formulas can be generalized to the cases where the baselines
have different weights.
It can be seen in the above formulas that the precision to which the
antenna phases and amplitudes is determined is improved by a factor 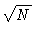 over the precision of the measurement of the baseline amplitudes and
phases.
over the precision of the measurement of the baseline amplitudes and
phases.




Next: 7.1.2 Gain corrections
Up: 7.1 Definitions and formalism
Previous: 7.1 Definitions and formalism
S.Guilloteau
2000-01-19
![]() should all be equal to the quasar flux
density S. Then
should all be equal to the quasar flux
density S. Then
![]() ,
the equations for phases are simply:
,
the equations for phases are simply:
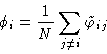
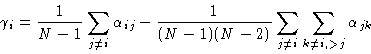
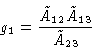
![]() over the precision of the measurement of the baseline amplitudes and
phases.
over the precision of the measurement of the baseline amplitudes and
phases.