



Next: 21. Mm versus Optical
Up: 20. Basic Principles of
Previous: 20.4 Accurate Position Measurements
Contents
Subsections
20.5 Sources of Position Uncertainty
We have given evidence that extended baselines are best for accurate position
measurements. In addition, as long as sensitivity is not an issue and that observed
sources are not resolved by the array, the outermost stations should always be preferred
(Section 20.4). The great asset of the IRAM array is clearly sensitivity coupled
with resolving power, although atmospheric fluctuations and instrumental limitations may
limit the accuracy of position measurements.
We further discuss below the boundary conditions or requirements in astrometric
observations. Table 2 at the end of this section summarizes the limitations with respect
to the IRAM array.
Among several practical limitations it is worth mentioning: wind effects, thermal
effects in the antenna structure (including de-icing instabilities), the influence of
refraction effects, imperfections in subreflector displacements, imperfections in the
azimuth and elevation bearings of the antennas and, not least, uncertainties in the
``crossing point" of the azimuth and elevation axes. These imperfections, and in fact the
resulting differential effects of each antenna pair in the array, have adverse effects on
the visibility phase measurements; however, many of them can be removed to a large extent
by phase calibration (a posteriori), and thus will not be discussed further.
In order to make the reader more aware of these questions, we just mention that the
large-scale uneveness of the azimuth bearings gives rise, in places, to optical path
deviations of about 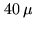 m which translate into position offsets of
m which translate into position offsets of 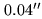 with 200m
baselines. Likewise, position uncertainties result from imperfections in the ``crossing
point" of the azimuth and elevation (nodal point) of each antenna in the array (see
Chapter 6). Slow drifts in the focal position are also corrected to first order by the
calibration procedure. Only large and rapid focal drifts are problematic if not recognized
as such in the phase of a reference calibrator.
with 200m
baselines. Likewise, position uncertainties result from imperfections in the ``crossing
point" of the azimuth and elevation (nodal point) of each antenna in the array (see
Chapter 6). Slow drifts in the focal position are also corrected to first order by the
calibration procedure. Only large and rapid focal drifts are problematic if not recognized
as such in the phase of a reference calibrator.
We elaborate here on some properties of the IRAM array related to inaccuracies in the
determination of baseline lengths, and we briefly discuss how atmospheric phase noise and
source strength can limit the accuracy of position measurements.
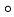
- Baselines: are easily measured with the IRAM interferometer on
Plateau de Bure with a precision of a few degrees or a small fraction of one millimetre.
As a reference, good winter conditions allow us to measure baselines at 86GHz, using a
number of quasars well-distributed in hour-angle and declination, with uncertainties of
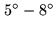 in the D configuration (the most compact one at IRAM) and
in the D configuration (the most compact one at IRAM) and
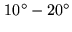 in the A configuration. But even the most accurate baseline
measurement will be limited in precision. Residual uncertainties in the baselines will
finally produce phase errors that scale with
in the A configuration. But even the most accurate baseline
measurement will be limited in precision. Residual uncertainties in the baselines will
finally produce phase errors that scale with
 , the distance between a calibration quasar and the source.
Combining the different forms of the phase equation defined in Section 20.2, we
can then derive a rough estimate of the mean uncertainty in the absolute position of a
source from
, the distance between a calibration quasar and the source.
Combining the different forms of the phase equation defined in Section 20.2, we
can then derive a rough estimate of the mean uncertainty in the absolute position of a
source from
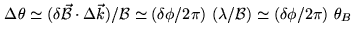 |
(20.22) |
where
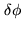 is the phase error due to inaccuracies in the baselines. This formula
is convenient, as it associates uncertainties in the knowledge of the baseline length at a
given frequency with
is the phase error due to inaccuracies in the baselines. This formula
is convenient, as it associates uncertainties in the knowledge of the baseline length at a
given frequency with 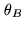 , the synthesized beam. For instance, observations at
86GHz in the D configuration with baseline phase residuals
, the synthesized beam. For instance, observations at
86GHz in the D configuration with baseline phase residuals
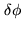 between
between
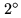 and
and 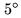 (i.e. assuming baseline errors,
(i.e. assuming baseline errors,
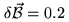 mm,
and typical phase calibrator distances,
mm,
and typical phase calibrator distances,
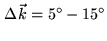 ) appear to have
position uncertainties smaller than
) appear to have
position uncertainties smaller than 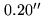 . See Subsection 20.4.2 for
suggestions to improve these uncertainties.
. See Subsection 20.4.2 for
suggestions to improve these uncertainties.
- Atmospheric phase fluctuations are among the most important
limitations that affect the accuracy of position measurements. Poor seeing conditions
imply phase decorrelation which in turn implies reduced flux density sensitivity and
larger apparent source sizes (see Chapters 9 and 10). When the atmospheric phase noise
dominates, phase decorrelation can be estimated by least-square fitting in time the phase
profile of a reference calibrator. Under the assumptions made at the end of Section
20.3 or assuming here that the atmospheric phase fluctuations remain unchanged,
namely
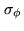 is similar for each phase sample, we can estimate the mean angular
uncertainty from
is similar for each phase sample, we can estimate the mean angular
uncertainty from
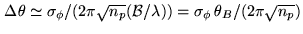 |
(20.23) |
where 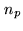 is the number of phase samples. The size of the associated ``seeing disk"
is defined as
is the number of phase samples. The size of the associated ``seeing disk"
is defined as
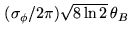 . For instance, measuring
mean atmospheric phase fluctuations
. For instance, measuring
mean atmospheric phase fluctuations
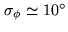 at 86GHz on a 60m
baseline is equivalent to observe in
at 86GHz on a 60m
baseline is equivalent to observe in
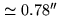 seeing conditions (which is small
since
seeing conditions (which is small
since
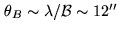 and corresponds to a small fraction
of the synthesized beam). Observations at the same frequency, on the same baseline and
with similar atmospheric conditions will then provide a position accuracy of order
and corresponds to a small fraction
of the synthesized beam). Observations at the same frequency, on the same baseline and
with similar atmospheric conditions will then provide a position accuracy of order
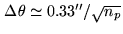 (or
(or 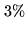 of
of
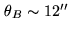 ).
).
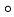
- Source strength and finite signal to noise ratio is another important
limitation to astrometric accuracy. While reference calibrators have to provide enough
sensitivity for rapid detection, detection of program sources may require hours of
integration. In addition, observed sources are sometimes resolved out with extended
configurations. Therefore, the interesting astrometric case described in Section
20.4 where spectral sources are rather easily detected may not be common in
mm-wave astronomy. As mentioned in Section 20.4.2 we can use the result of
[Reid et al. 1988] to estimate the one sigma position uncertainty
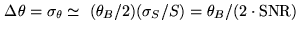 |
(20.24) |
where 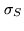 is the noise in the map and
is the noise in the map and 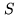 the source flux density. With the IRAM
array in the D configuration, a source at mean declination (e.g.
the source flux density. With the IRAM
array in the D configuration, a source at mean declination (e.g.
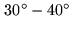 )
detected with a signal-to-noise SNR
)
detected with a signal-to-noise SNR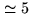 , cannot be located with a precision better
than
, cannot be located with a precision better
than 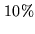 of
of 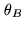 (e.g.
(e.g. 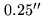 at 230 GHz). Uncertainties in declination
measurements will obviously be larger for southern sources owing to the elongation of the
synthesized beam.
at 230 GHz). Uncertainties in declination
measurements will obviously be larger for southern sources owing to the elongation of the
synthesized beam.
On the other hand, astrometric observations of bright sources such as the SiO line
sources presented in Section 20.4 are not limited by SNR issues in general, but
by the accuracy of the bandpass calibration. While delay calibration (see Chapter 5)
already removes the bulk of the phase gradient across the band selected for observations,
residual variations can only be removed by observing strong calibrators. Using the
classical radiometric equation, bandpass calibration requires the following:
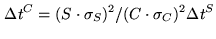 |
(20.25) |
In this expression, 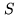 and
and 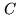 are the flux densities of the source and calibrator,
are the flux densities of the source and calibrator,
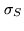 and
and 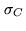 the respective r.m.s. noise levels, and
the respective r.m.s. noise levels, and
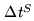 and
and
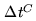 the integration times on the source and calibrator. For instance, a 1sec
integration on a 15Jy calibrator like 3C273 (at the time of writing, the strongest
calibrator at 86GHz available in the northern sky) is sufficient for bandpass
calibration in the case of a
the integration times on the source and calibrator. For instance, a 1sec
integration on a 15Jy calibrator like 3C273 (at the time of writing, the strongest
calibrator at 86GHz available in the northern sky) is sufficient for bandpass
calibration in the case of a 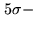 detection of a 2mJy source. (In practice,
however, several seconds integration would be better.) On the other hand, a 10min
integration on the same calibrator would just be sufficient to meet the minimum
requirement (
detection of a 2mJy source. (In practice,
however, several seconds integration would be better.) On the other hand, a 10min
integration on the same calibrator would just be sufficient to meet the minimum
requirement (
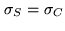 ) to calibrate 1min observations of a 50Jy strong
source.
) to calibrate 1min observations of a 50Jy strong
source.
There are a few other issues which we list below. They are worth mentioning although there
is little implication for observations with the IRAM array. (For other effects such as
bandwidth smearing and visibility averaging, we recommend reading the book of
[Thompson et al. 1986]; see Chapter 6.)
- Pointing offsets is a potential source of position errors. Ideally,
the phase of the incoming wavefront does not depend on pointing offsets across the Airy
(or diffraction) pattern. However, imperfections in the optical system may result in
differences in the Airy pattern from an antenna to another in the array (although all
antennas are of comparable quality). Experience at 86GHz shows, that rather strong
phase differences (up to
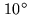 ) may appear when antennas are individually offset from
the target position by a distance equal to half the primary beamwidth (HPBW).
) may appear when antennas are individually offset from
the target position by a distance equal to half the primary beamwidth (HPBW).
- Primary beam attenuation produces a radial displacement for off-axis
targets. It needs to be corrected for targets at large angular distances (
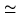 HPBW/2)
from the phase tracking center of the interferometer.
HPBW/2)
from the phase tracking center of the interferometer.
- Gravitational Lensing by the Sun introduces positional offsets
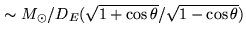 which
are negligible for targets outside the Sun avoidance region of the
IRAM antennas (
which
are negligible for targets outside the Sun avoidance region of the
IRAM antennas (
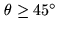 ). For instance
). For instance
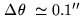 at
at
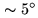 from the Sun limb.
from the Sun limb.
A summary of the main practical position uncertainties for the IRAM array is given in
Table 2 in arc second or in terms of the synthesized beam 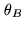 ;
; 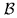 is the
baseline length in meter. Only instrumental errors are removed to first order by
calibration.
is the
baseline length in meter. Only instrumental errors are removed to first order by
calibration.
Table 2. Plateau de Bure Interferometer - Main Sources of Position Uncertainty
| |
|
|
TELESCOPE |
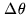 |
Calibration |
| |
|
|
| Focus Offset |
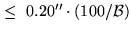 |
Yes |
| Axes Non-Intersection |
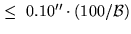 |
Yes |
| AzEl Bearings |
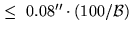 |
Yes |
| |
|
|
| OBSERVATION |
|
|
| |
|
|
Atmospheric Seeing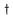 |
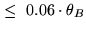 |
No |
Calibrator Distance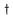 |
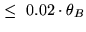 |
No |
| Pointing Offset |
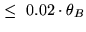 |
Partially |
| Source Intensity |
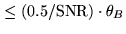 |
No |
| |
|
|
 Upper limits are illustrative for astrometric
observations in limiting conditions. See text for more details.
Upper limits are illustrative for astrometric
observations in limiting conditions. See text for more details.
 Instrumental values are all calibrated out to first
order.
Instrumental values are all calibrated out to first
order.




Next: 21. Mm versus Optical
Up: 20. Basic Principles of
Previous: 20.4 Accurate Position Measurements
Contents
Anne Dutrey
![]() m which translate into position offsets of
m which translate into position offsets of ![]() with 200m
baselines. Likewise, position uncertainties result from imperfections in the ``crossing
point" of the azimuth and elevation (nodal point) of each antenna in the array (see
Chapter 6). Slow drifts in the focal position are also corrected to first order by the
calibration procedure. Only large and rapid focal drifts are problematic if not recognized
as such in the phase of a reference calibrator.
with 200m
baselines. Likewise, position uncertainties result from imperfections in the ``crossing
point" of the azimuth and elevation (nodal point) of each antenna in the array (see
Chapter 6). Slow drifts in the focal position are also corrected to first order by the
calibration procedure. Only large and rapid focal drifts are problematic if not recognized
as such in the phase of a reference calibrator.
![]() ;
; ![]() is the
baseline length in meter. Only instrumental errors are removed to first order by
calibration.
is the
baseline length in meter. Only instrumental errors are removed to first order by
calibration.