

Next: Coordinates and Velocities
Up: Call for Observing Proposals
Previous: Receivers
The rms noise can be computed from
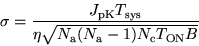 |
(1) |
where
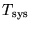 is the mean system temperature in
is the mean system temperature in 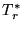 scale
(150K below 110GHz, 300K at 115GHz, 500K at 230GHz
for sources at
scale
(150K below 110GHz, 300K at 115GHz, 500K at 230GHz
for sources at
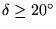 ),
),
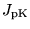 is the conversion factor from Kelvin to Jansky (22
at 3mm, 35 at 1.3mm),
is the conversion factor from Kelvin to Jansky (22
at 3mm, 35 at 1.3mm),
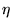 is an efficiency factor due to atmospheric phase noise
(0.9 at 3mm, 0.8 at 1.3mm),
is an efficiency factor due to atmospheric phase noise
(0.9 at 3mm, 0.8 at 1.3mm),
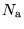 is the number of antennas (5), and
is the number of antennas (5), and 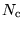 is
the basic number of configurations (1 for D, 2 for CD, and
so on)
is
the basic number of configurations (1 for D, 2 for CD, and
so on)
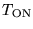 is the integration time per configuration
in seconds (2 to 8 hours, depending on source
declination). Because of calibrations and antenna slew time,
the effective (on-source) integration time is about 60-70% of the
total
observing time,
is the integration time per configuration
in seconds (2 to 8 hours, depending on source
declination). Because of calibrations and antenna slew time,
the effective (on-source) integration time is about 60-70% of the
total
observing time,
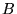 is the channel bandwidth in Hz (580 MHz for continuum, 40
kHz to 2.5 MHz for spectral line, according to spectral
correlator setup).
is the channel bandwidth in Hz (580 MHz for continuum, 40
kHz to 2.5 MHz for spectral line, according to spectral
correlator setup).
Investigators have to specify the one sigma noise level which is
necessary to achieve each individual goal of a proposal, and
particularly for projects aiming at deep integrations.


Next: Coordinates and Velocities
Up: Call for Observing Proposals
Previous: Receivers
Clemens Thum
2006-02-01