A Fast-Mapping Method for Bolometer Arrays: Commissioning tests

Introduction

In the August 1999 IRAM Newsletter we presented a ``fast-mapping method'' for array receivers at the 30-m Telescope (see [1]). After initial successful tests, there were some open questions left, like: `Do we observe any beam broadening due to fast mapping? How does the noise in a map decrease with increasing integration time?' Furthermore we want to demonstrate this method by doing a large map of more than an hour integration time. With this questions in mind we applied for test time. The results are summarized below.

  

Figure 1: An example of mapping a faint source in two different ways. In Fig. a four fast coverages are averaged, in b a single 'normal' coverage is shown. In Fig. c the measured RMS noise is shown obtained in 1, 2, 3 and 4 `fast' maps as well as for the 'normal' map and the average of all 5 maps is shown. The line shown has a slope of -1, indicating that the RMS noise reaches the confusion limit for the longest integration.

  

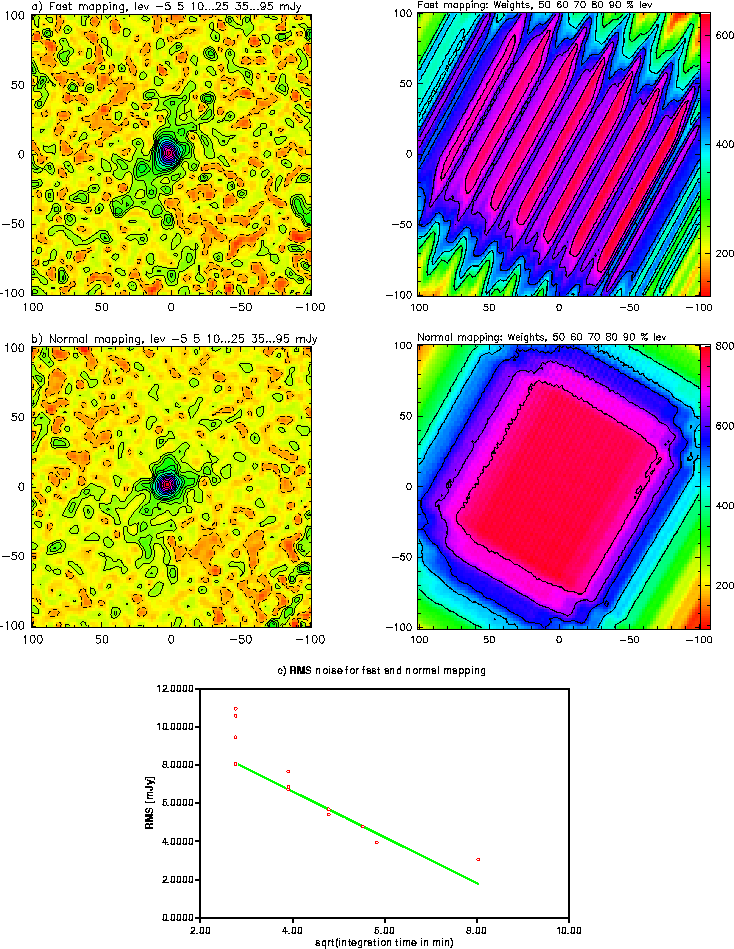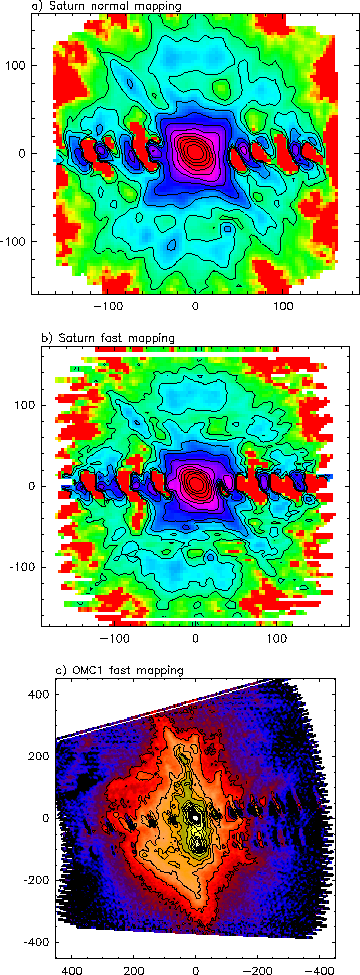
Figure 2: a shows a `normal' map and b a fast map of Saturn. The contour levels are 0.05, 0.1, 0.2, 0.4, 0.8, 1.6, 3.2, 6.4, 12.8, 25.6 and 50% of the peak. Figure c shows a 13.5 by 10 arc minute map of Orion OMC1. The contour levels correspond to 0.5, 1, 2, 3, 4, 6, 8, 10, 15 ... 50 by 5% of the peak brightness.

The method

This method works best with closely packed hexagonal arrays. There is no need to de-rotate the array or to choose a particular scanning direction. Here we apply this method to the MPIfR 37-channel bolometer MAMBO II mounted in the Nasmyth focus of the IRAM 30-m. From Fig. 1 of our previous report [1], we may distinguish two different arrangements of pixels:

• At 30 and 90 degrees elevation we have 7 rows with a separation $D=18\hbox{$^{\prime\prime}$ }$. In order to obtain a map sampled $\delta =4\hbox{$^{\prime\prime}$ }$ in elevation we choose an increment in elevation of $\Delta E=D+\delta=22\hbox{$^{\prime\prime}$ }$. Consider a single scan-line (subscan). For simplicity let the first row of the array be at elevation offset 0, we can write down the following table of elevation offsets for three subscans:

  
  
  
  
  

  sub-	row	row	row	...	row
  scan	n	n-1	n-2	...	n-7
  1	0	-D	-2D	...	-7D
  2	$D+\delta$	$\delta$	-$D+\delta$	...	- $6D+ \delta$
  3	$2(D+\delta)$	$D+2\delta$	$2\delta$	...	- $5D+ 2\delta$
  $\vdots$

  
  
  
  and so on. We see that after 6 subscans we have sampled the elevation offset $5\delta$ and thus the final map will be fully sampled in elevation. Thus the minimum map size in elevation is 6 subscans and the array should have more than 6 rows.

• At 0 and 60 degrees elevation we have 13 rows with a separation $0.56\,D \sim 10\hbox{$^{\prime\prime}$ }$. An increment of $22\hbox{$^{\prime\prime}$ }$ in elevation results in a map sampled better than $2\hbox{$^{\prime\prime}$ }$ where the gaps are filled in with every other row of pixels. Here we also need 6 subscans or more and more than 11 rows of pixels.

Observations

On 12th February 2000 we had 7 hours of observing time. During the first hour the weather was too bad to observe, afterwards the opacity improved rapidly (tau 0.12 at the end of the session!) A rapid change in opacity often indicates that the atmosphere is not yet settled, indeed, we had some anomalous refraction that led to the large restoration residuals visible in the maps of the strong sources (see Fig. 2). All maps were done chopping the sub-reflector at a little less than 2 Hertz, scanning in Azimuth at $6\hbox{$^{\prime\prime}$ }$ per second. For the normal maps we used $4\hbox{$^{\prime\prime}$ }$ as increment in elevation and $22\hbox{$^{\prime\prime}$ }$ for all fast maps.

Results

We have mapped a weak point-like source of about 80 mJy peak flux density several times, once using ``normal mapping'' and four times using ``fast mapping'' All four fast maps were averaged and the result shown in Fig.1a. The normal map, shown in Fig.1b, is equivalent to 11% more integration time compared to the average of 4 fast maps. On the right side we show the distribution of weights in the map, it is proportional to the number of points added per unit area, which in turn is proportional to the integration time. From this distribution we see that it is of advantage to map the same field at several hour angles, in particular for fast mapping as the distribution is not very uniform. In case of ``deep'' mapping the wider distribution of weights in a fast map may be of advantage and at the end may lead to a less centered distribution of weights. Mapping the same field in azimuth and elevation leads to a larger area mapped, say with weights > 90%. We computed the RMS noise in the maps over a small `source free' region near the center of a map. The resulting RMS noise is shown for some combination of maps in Fig.1c. From left to right the resulting noise for the average of 1, 2, 3 and 4 fast maps, the normal map and the average of all maps is plotted against $\sqrt{(integration\ time\ in\ minutes)}$. The flattening of the slope near the end may well indicate the confusion limit, which is probably quite high since some faint extended emission is visible in this field.

In Figure 2 we show a normal and a fast map of Saturn (Fig. 2a and b). The maps were interpolated onto a Azimuth/Elevation grid. The diagonal elongated structures are caused by the quadripod sub-reflector support legs, these merge into a patchy ring of emission with diameter about $200\hbox{$^{\prime\prime}$ }$. These features agree well with those seen in holography maps, in spite of large disk of Saturn ( $18\hbox{$^{\prime\prime}$ }$ by $16\hbox{$^{\prime\prime}$ }$). The main beam is also well reproduced in the fast maps, comparing Gaussian fits to the main beam in our four Saturn maps showed a total variation of about 2%. This could easily be caused by changes in the opacity and we can only say that we did not detect any deterioration of the main beam due to fast mapping.

Finally in Fig. 2c we show a fast map of OMC1 in Orion. In Azimuth/Elevation we mapped a region of $800\hbox{$^{\prime\prime}$ }$ by $600\hbox{$^{\prime\prime}$ }$. At a scanning speed in azimuth of $6\hbox{$^{\prime\prime}$ }/$sec each subscan took about 133 seconds. With a spacing in elevation of $22\hbox{$^{\prime\prime}$ }$ the whole map consisted only of 29 subscans and took a little over 64 minutes to complete.

The Future

We successfully demonstrated a fast mapping method for closely packed hexagonal arrays with more than 19 pixels. This method will gain from more pixels, i.e. the weight distribution will be wider for fast maps and narrower for normal maps when comparing the upcoming 117 pixel bolometer array to the 37 pixel array.

One can improve the double beam restoration by combining the data of several fast maps done with different chopper throws by using a improved restoration method as described by Emerson and Payne 1995 [2].

Obviously this method can be used also with a fast scanning total power mode developed by the MPIfR in Bonn. In this case, a four-fold increased scanning speed of $24\hbox{$^{\prime\prime}$ }$ per second would allow to cover the region of the OMC1 map in Fig. 2 in 16 Minutes. You could map the full moon in about 1.5 hours!

Bibliography

[1]

David Teyssier, Albrecht Sievers 1999, IRAM Newsletter Aug 1999 (http://www.iram.es/Telescope/manuals/Report/Fast_bolo.ps)

[2]

Emerson, D.T., Payne,J.M., 1995, Multi-Feed Systems for Radio-Telescopes, PASP, Vol. 75, p. 332

Albrecht SIEVERS and David TEYSSIER