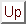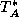 , the `antenna temperature
corrected for rear spillover losses and atmospheric attenuation'. The r.m.s.
noise fluctuation is then:
, the `antenna temperature
corrected for rear spillover losses and atmospheric attenuation'. The r.m.s.
noise fluctuation is then:

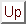


Since we use the chopper wheel method for calibration, it is convenient to
write the radiometer equation in units of 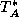 , the `antenna temperature
corrected for rear spillover losses and atmospheric attenuation'. The r.m.s.
noise fluctuation is then:
, the `antenna temperature
corrected for rear spillover losses and atmospheric attenuation'. The r.m.s.
noise fluctuation is then:
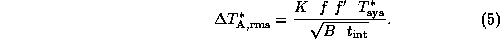
 (in seconds) the sum of the
integration times ON the source and on the OFF position. This time does not
take into account additional times due to telescope movement and data handling.
For standard observations, the same amount of time is spent on the source and
on a reference field (the raster mode can be different).
(in seconds) the sum of the
integration times ON the source and on the OFF position. This time does not
take into account additional times due to telescope movement and data handling.
For standard observations, the same amount of time is spent on the source and
on a reference field (the raster mode can be different).
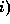 equal to half the linewidth, or
equal to half the linewidth, or 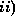 equal to 50 MHz,
whichever is the smallest (weak lines broader than 50 MHz, in fact, are more
difficult to detect than 50 MHz-wide lines).
equal to 50 MHz,
whichever is the smallest (weak lines broader than 50 MHz, in fact, are more
difficult to detect than 50 MHz-wide lines).
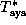 is the system temperature (K) (see below)
is the system temperature (K) (see below)
 is spent on the source itself and that
a substraction ON-OFF will be made. For frequency switched observations K
equals
is spent on the source itself and that
a substraction ON-OFF will be made. For frequency switched observations K
equals 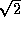 since all the time is spent on the source. The factor f is
1.15 for the autocorrelator, 1.0 for the filterbank (see above). The factor
since all the time is spent on the source. The factor f is
1.15 for the autocorrelator, 1.0 for the filterbank (see above). The factor
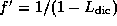 is due to losses in the dichroic mirror.
is due to losses in the dichroic mirror.
The system temperature 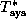 (in the
(in the 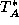 scale) is calculated by
OBS via
scale) is calculated by
OBS via
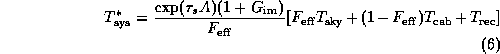
with the mean physical atmospheric temperature (see [2]) ¯, and
with the zenith opacity in the signal sideband
,
the airmass
,
the sideband gain ratio (see Table 2)
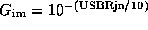
the sky brightness temperature
,
the mean physical atmospheric temperature (see [2])
,
the ambient temperature
, and
the receiver temperature (see Table 2)
.
Zenith opacities are strongly correlated with the most important atmospheric absorbant, water; the relevant parameter is the amount of precipitable water vapour (pwv --see [2],[3]). For 20% of the time during winter (summer) the pwv is below 2 mm (4 mm). The `average' pwv is below 4 mm during the winter regime and below 7 mm during the summer regime (see e.g. IRAM technical reports [2],[4]). Zenith opacities for typical winter and summer conditions are given in Table 3.

Table:
Zenith opacities for typical weather conditions at selected frequencies
Note that January and February are dedicated in principle to 0.8 mm and bolometer observations. Especially during this period the night-time opacities are better than the day-time opacities.
Table 4 gives examples of the rms noise 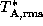 after 10
minutes of total integration time (ON + OFF position). To calculate the system
temperature some typical values were chosen: Elevation
after 10
minutes of total integration time (ON + OFF position). To calculate the system
temperature some typical values were chosen: Elevation 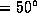 , gain
ratio
, gain
ratio 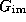 between 0.001 and 1 (depending on receiver and frequency),
forward efficiency
between 0.001 and 1 (depending on receiver and frequency),
forward efficiency 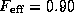 , cabin temperature
, cabin temperature 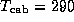 K,
mean atmospheric temperature
K,
mean atmospheric temperature 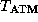 = 250 K.
= 250 K.
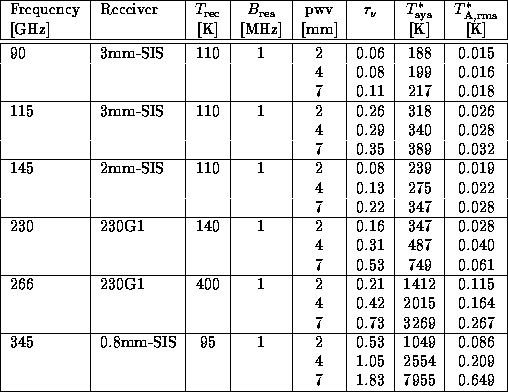
Table:
Examples of rms noise values after 10 minutes of integration (assuming
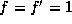 )
)