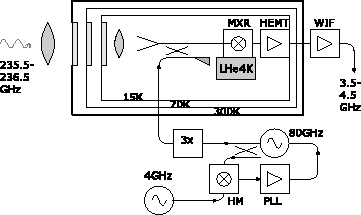
Figure 2: Synoptic diagram of a typical receiver. This diagram is grossly simplified; for instance, the optics involves mirrors, elliptical and planar, and also grids; the LO/PLL system is actually more complicated than shown.
The purpose of a receiver is to collect efficiently the astronomical signal that has been concentrated by the antenna near its focal point, and to amplify it with a minimum of extra noise to a level suitable for further processing by the spectrometers or continuum detectors. Figure 2 shows the main subsystems of a receiver, that we will discuss below.

Figure 2: Synoptic diagram of a typical receiver. This diagram is grossly
simplified; for instance, the optics involves mirrors, elliptical and
planar, and also grids; the LO/PLL system is actually more complicated than
shown.
Up to and including the antenna, the astronomical signal propagates in free space. On the other hand, the first signal processing unit --the mixer-- requires the electromagnetic energy to be confined by metallic walls, in a waveguide. The transition between these two modes of propagation occurs at the horn.

Figure 3: A corrugated horn for the 150GHz band. The phase-correcting lens
normally present at the aperture has been removed to reveal the
corrugations. The diameter of the aperture is about that of a typical coin
(1DM/100Ptas/1F). All the waves collected by the 30-m antenna converge to
the horn with a precise phase relationship and are then squeezed into a
waveguide ![]() mm across.
mm across.
Assume for a moment that the horn would be placed at the Cassegrain focus of the antenna. Good matching would be difficult to achieve because the field amplitude from a point source (Airy pattern) exhibits radial oscillations alternating between positive and negative values, and has a scalesize proportional to wavelength.
These problems are avoided by coupling --via suitable relay optics-- the horn to an image of the aperture. This fulfills the condition of frequency-independent illumination. In other words, imagine that we propagate the horn mode back to the antenna aperture as if we were dealing with a transmitter, then the illumination pattern is independent of frequency. Using suitably designed corrugations on the inner wall of the horn (see fig. 3) the TE10 mode of the rectangular waveguide couples to a mode at the aperture of the horn whose amplitude has circular symmetry, and whose polarization is pure linear.
In the present context, heterodyne refers to receivers where the frequency of the input signal is shifted to lower frequencies. This is done by adding to the (small) input signal a (relatively) strong monochromatic signal, called the local oscillator and passing the sum through a non-linear device, whose output contains (among other) the difference frequency. Although a non-linear device is involved, the transformation from input to output is linear for the small signal. This process is called mixing or downconversion. The output signal is called the intermediate frequency. Actually the complete signal processing at a radiotelescope can involve up to four heterodyne conversions.
The first reason why heterodyne downconversion is needed is that only few signal processing devices exist at millimeter frequencies, and definitely not the fully parallel spectrometers (as opposed to multiplex devices such as FTS) that are routinely used for spectroscopic observations.
Then arises the question of where in the signal processing chain to make the down conversion. Basically we have no choice, because hardly any amplifiers are available in the millimeter range, except in the 3mm band, where they do not match the low noise properties of SIS mixers (to be discussed below). So we must perform a downconversion before we can amplify the signal.
All the local oscillators in the IRAM telescopes use Gunn oscillators.
A Gunn diode is a semiconductor device that exhibits negative dynamic
resistance over a suitable range of frequencies. Output powers of the
order of 10-50mW can be obtained between 60 and 120 GHz. To achieve
oscillation at a precise frequency, two means are combined. First, the
Gunn diode is coupled to a coaxial cavity that defines the oscillation
frequency, and whose high quality factor provides a good spectral purity.
Its resonant frequency can
be adjusted mechanically; this allows the desired frequency to be
approached within ![]() 10 MHz. Secondly, a fraction of the
millimetric radiation from the Gunn oscillator is used to produce a beat
with a reference microwave oscillator at a frequency of a few GHz;
actually, the Gunn oscillator signal beats with a harmonic (n=17-65,
depending on the systems) of the reference frequency. The beat signal is
used to ``servo'' by electronic tuning the Gunn oscillator to a multiple
of the reference. Actually, not only the frequency, but also the phase
of the local oscillator is locked to the reference oscillator, which is
essential for interferometry, whether connected-array or VLBI.
This description of the phase-lock system is over-simplified.
10 MHz. Secondly, a fraction of the
millimetric radiation from the Gunn oscillator is used to produce a beat
with a reference microwave oscillator at a frequency of a few GHz;
actually, the Gunn oscillator signal beats with a harmonic (n=17-65,
depending on the systems) of the reference frequency. The beat signal is
used to ``servo'' by electronic tuning the Gunn oscillator to a multiple
of the reference. Actually, not only the frequency, but also the phase
of the local oscillator is locked to the reference oscillator, which is
essential for interferometry, whether connected-array or VLBI.
This description of the phase-lock system is over-simplified.
Local oscillator frequencies above 120GHz can generally not be generated
directly by Gunn oscillators. In that case, the Gunn power is fed to a
frequency multiplier, which is a non-linear device like the
mixer, but based on non-linear capacitance, and optimized to produce a
certain harmonic ( ![]() ,
, ![]() or
or ![]() in the case of
IRAM systems) of the input frequency. The efficiency of the
multiplication process is typically a few percent.
in the case of
IRAM systems) of the input frequency. The efficiency of the
multiplication process is typically a few percent.
As mentioned above, the local oscillator power must be added to the astronomical signal before it enters the mixer. When the mixers were based on Schottky diodes (10 years ago and more), they required an LO power of almost a mW. As a consequence, the LO power was coupled via a diplexer, which is like a frequency-selective coupler, allowing the mixer to be coupled with close to unity efficiency to both the input signal and the LO. With the advent of SIS mixers, and due to their modest LO power requirements (read below), a new method can be used, based on frequency-independent couplers. A fraction f (typically 1%) of the LO power is coupled into the signal path; the rest is wasted! The fraction f must be kept small because the same amount f of room-temperature blackbody noise is also coupled into the signal path. The coupler requires no adjustment and is located close to the receiver, inside the cryostat (discussed below).
All mixers in IRAM receivers are based on SIS junctions. An SIS junction
consists of two layers of superconducting metal (Niobium) separated by a
few nanometers of insulator (Aluminium oxide). The insulator is so thin
that charged particles can tunnel through the barrier. The area of a
junction is typically one to a few ![]() . SIS junctions operate at the
boiling temperature of He: 4.2K (at sea level).
. SIS junctions operate at the
boiling temperature of He: 4.2K (at sea level).
Two kinds of charged particles can exist in a superconductor:
a) ordinary electrons; b) so-called Cooper pairs, consisting of two
electrons interacting and weakly bound together by the exchange of
phonons (lattice vibrations); breaking a Cooper pair costs an energy
![]() . Correspondingly, two kinds of currents can
flow across the junction: the Josephson current, consisting of Cooper
pairs, and the so-called quasi-particle current, consisting of
``ordinary'' electrons (presumably ``electron'' did not sound fancy
enough). To keep this digression into SIS physics short, let's just
state that the Josephson current can be ignored. At the operating
temperature of the mixer, and in an unbiased junction, the population of
quasi-particles is virtually negligible. But, if the bias voltage is
raised to the gap voltage
. Correspondingly, two kinds of currents can
flow across the junction: the Josephson current, consisting of Cooper
pairs, and the so-called quasi-particle current, consisting of
``ordinary'' electrons (presumably ``electron'' did not sound fancy
enough). To keep this digression into SIS physics short, let's just
state that the Josephson current can be ignored. At the operating
temperature of the mixer, and in an unbiased junction, the population of
quasi-particles is virtually negligible. But, if the bias voltage is
raised to the gap voltage
![]()
the flow of quasi-particles across the junction becomes possible because the energy gained across the drop of electrical potential compensates for the energy spent in breaking a Cooper pair. See in Figure 4 the ``LO off'' I-V characteristic.
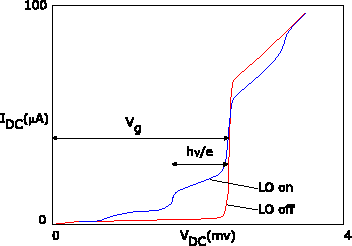
Figure 4: Current-voltage characteristics of an SIS junction operating in a
mixer. The two curves were measured without and with LO power applied
(frequency 230GHz); they have been slightly idealized (for pedagogical
reasons, of course).
In the presence of electromagnetic radiation, the situation is modified
as follows. If a RF photon is absorbed, its energy ![]() can contribute
to the energy budget, which can now be written as:
can contribute
to the energy budget, which can now be written as:
![]()
or, equivalently:
![]()
In other words, the onset of conduction occurs at ![]() . The
region of the I-V curve below the gap voltage where photon-assisted
tunneling occurs is called the photon step. See the ``LO on''
curve in Figure 4. Figure 4 is based on actual
measurements of a 2-junction series array: the voltage scale has been
scaled
. The
region of the I-V curve below the gap voltage where photon-assisted
tunneling occurs is called the photon step. See the ``LO on''
curve in Figure 4. Figure 4 is based on actual
measurements of a 2-junction series array: the voltage scale has been
scaled ![]() to illustrate a single junction.
SIS junctions and their interaction with radiation will be analyzed
in more detail in a review by K. Schuster to appear
in the next IRAM Newsletter (April 1999).
to illustrate a single junction.
SIS junctions and their interaction with radiation will be analyzed
in more detail in a review by K. Schuster to appear
in the next IRAM Newsletter (April 1999).
So far I've shown you qualitatively that an SIS junction can function as
a total power detector. The responsivity (current generated per power
absorbed) can even be estimated to be of the order of one electron per
photon, or: ![]() . How does that relate to frequency
downconversion? Assume that a power detector is fed the sum of a local
oscillator (normalized to unit amplitude for convenience)
. How does that relate to frequency
downconversion? Assume that a power detector is fed the sum of a local
oscillator (normalized to unit amplitude for convenience)
![]() and a much smaller signal at a
nearby frequency:
and a much smaller signal at a
nearby frequency: ![]() . Assume this functions
as a squaring device and discard high-frequency terms in the output:
. Assume this functions
as a squaring device and discard high-frequency terms in the output:
![]()
So, a power detector can also function as a frequency downconverter (subject to possible limitations in the response time of the output).
The LO power requirement for an SIS mixer can be estimated as follows. A
voltage scale is defined by the width of the photon step: ![]() .
Likewise, a resistance scale can be defined from
.
Likewise, a resistance scale can be defined from ![]() , the resistance of
the junction above
, the resistance of
the junction above ![]() ; junctions used in mixers have
; junctions used in mixers have ![]() . So, the order of magnitude of the LO power required is:
. So, the order of magnitude of the LO power required is:
![]()
about 20 nW for a 230 GHz mixer. This makes it possible to use the wasteful coupler injection scheme discussed above.
Because the insulating barrier of the junction is so thin, it possesses a
capacitance of about ![]() . At the RF and LO frequencies, the
(imaginary) admittance of that capacitance is about 3-4
. At the RF and LO frequencies, the
(imaginary) admittance of that capacitance is about 3-4 ![]() the
(approximately real) admittance of the SIS junction itself. Therefore,
appropriate tuning structures must be implemented to achieve a good
impedance match (i.e. energy coupling) of the junction to the signals.
the
(approximately real) admittance of the SIS junction itself. Therefore,
appropriate tuning structures must be implemented to achieve a good
impedance match (i.e. energy coupling) of the junction to the signals.
The minimum theoretical SSB noise for an SIS mixer is ![]() , 11K at
230GHz; the best IRAM mixers come within a factor of a few
(
, 11K at
230GHz; the best IRAM mixers come within a factor of a few
( ![]() ) of that fundamental limit. These numbers are for
laboratory measurements with minimal optics losses; practical receivers
have a slightly higher noise.
) of that fundamental limit. These numbers are for
laboratory measurements with minimal optics losses; practical receivers
have a slightly higher noise.
A sketch of a mixer is shown in Figure 5, again grossly over-simplified. The junction is mounted across the wave-guide, in the direction of the electric field. One side of the junction is connected to the outside of the mixer block, both to bring out the IF beat signal, and to provide the DC bias. That connection is made through a low-pass filter to avoid losing precious RF energy.
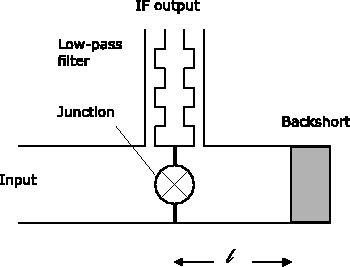
Figure 5: Rough sketch of the main elements of a mixer
One end of the waveguide is the input of the mixer; the other end must be terminated somehow. At the zero-order approximation, one would like the junction to ``see'' an open circuit when ``looking into'' the rear end of the waveguide. More generally, the junction should see a pure imaginary impedance, so that no energy is wasted. A simple calculation shows that a transmission line having a length l, and terminated into a short-circuit, has an apparent impedance:
![]()
where ![]() and
and ![]() are respectively the propagation
impedance and wavelength in the waveguide, and l is the distance to the
short-circuit. In particular, for
are respectively the propagation
impedance and wavelength in the waveguide, and l is the distance to the
short-circuit. In particular, for ![]() ,
the apparent impedance is an open circuit. More generally, by adjusting
l, an arbitrary imaginary impedance can be placed in parallel with the
junction. Together with the tuning structures mentioned in the previous
section, such an adjustable backshort
contributes to achieve the best possible match of the junction impedance.
,
the apparent impedance is an open circuit. More generally, by adjusting
l, an arbitrary imaginary impedance can be placed in parallel with the
junction. Together with the tuning structures mentioned in the previous
section, such an adjustable backshort
contributes to achieve the best possible match of the junction impedance.
For various reasons (one of which is reducing the noise contribution from
the atmosphere) it is desirable that the mixer should operate in
single-sideband mode. We explain how this is achieved with a crude
zero-order model. Assume that the best impedance match of the junction is
obtained when the apparent impedance of the backshort seen from the
junction is an open circuit. Assume we observe in the lower sideband at a
frequency ![]() , and want to reject the upper sideband
, and want to reject the upper sideband
![]() . That condition can be achieved if, at the
frequency
. That condition can be achieved if, at the
frequency ![]() , the junction is short-circuited. So, we must meet the two
conditions:
, the junction is short-circuited. So, we must meet the two
conditions:
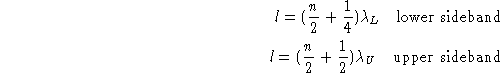
for some integer n; we gloss over the distinction between free-space and waveguide wavelengths. The two conditions (one unknown) can be approximately met for some l close to
![]()
In practice, single-sideband operation in the 100 GHz band requires additional tricks, because the IF frequency of the current 100 GHz mixers is relatively low (1.5 GHz).
Returning to practicalities, tuning a receiver requires several steps
(which used to make astronomers a bit nervous at the 30-m telescope when
all was done manually). First the local oscillator must be tuned and
locked at the desired frequency. Then the backshort is set at the
appropriate position, and the junction DC bias voltage is set. Finally the
LO power is adjusted to reach a prescribed junction DC current (of the
order of ![]() ). These adjustments are made by a combination of table
lookup and optimization algorithms under computer control. Altogether this
involves between 11 and 13 adjustments, mechanical or electrical, yet
this process takes only a few minutes with the current systems.
). These adjustments are made by a combination of table
lookup and optimization algorithms under computer control. Altogether this
involves between 11 and 13 adjustments, mechanical or electrical, yet
this process takes only a few minutes with the current systems.

Figure 6: The cold RF assembly for a dual-channel receiver used at the 30-m
telescope.
As mentioned earlier, the SIS junctions in the mixers operate at the
boiling temperature of He. Therefore, at the heart of the cryostat lies a
reservoir of ![]() 4 liters of liquid He. However, if that would be
exposed to ambient conditions, several undesirable things would happen.
First, conducted heat would quickly evaporate the helium. Second, a big
icicle of water, nitrogen, oxygen, etc...would condense around the
reservoir. Conduction and condensation are avoided by operating the
receiver in a vacuum enclosure (labelled 300K in
figure 2). But infrared radiation must also be blocked.
Your body is receiving about 700W from the surroundings! (and radiating back
about the same amount). A typical 4-liter reservoir of liquid He, exposed
to the same flux, would evaporate in 2 minutes! Yet the hold time of a
cryostat is one to several weeks, four orders of magnitude more. This is
achieved via the two radiation screens labelled 70K and 15K in
figure 2, as well as by reducing to a minimum all
conduction losses. The radiation screens are kept cold by a closed-cycle
cryogenic machine involving the compression and expansion of helium gas.
The 15K stage is also used to cool the first stages of IF amplification.
Future receivers will feature fully closed-cycle cryogenics, including the
4K stage.
4 liters of liquid He. However, if that would be
exposed to ambient conditions, several undesirable things would happen.
First, conducted heat would quickly evaporate the helium. Second, a big
icicle of water, nitrogen, oxygen, etc...would condense around the
reservoir. Conduction and condensation are avoided by operating the
receiver in a vacuum enclosure (labelled 300K in
figure 2). But infrared radiation must also be blocked.
Your body is receiving about 700W from the surroundings! (and radiating back
about the same amount). A typical 4-liter reservoir of liquid He, exposed
to the same flux, would evaporate in 2 minutes! Yet the hold time of a
cryostat is one to several weeks, four orders of magnitude more. This is
achieved via the two radiation screens labelled 70K and 15K in
figure 2, as well as by reducing to a minimum all
conduction losses. The radiation screens are kept cold by a closed-cycle
cryogenic machine involving the compression and expansion of helium gas.
The 15K stage is also used to cool the first stages of IF amplification.
Future receivers will feature fully closed-cycle cryogenics, including the
4K stage.
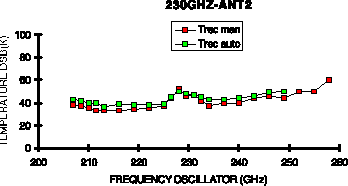
Figure 7: DSB noise performance of one of the 230GHz receivers in operation
at the PdB interferometer
Figure 6 gives you a chance to peek at the cold RF assembly of one of the dual-channel receivers in operation at the 30-m telescope since May 1998.
Figure 7 shows the performance of one of the Plateau de Bure 230GHz receivers. The present LO/IF system dictates a 1.5GHz IF, therefore, these receivers are operated in DSB mode; in the interferometer, the sidebands can be separated due to their different fringe rates.
B.Lazareff