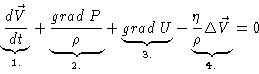 |
(9.2) |
Scepticism was nourished by the fact that some stationary (i.e. time invariant) solutions were mathematically valid but not observed experimentally, which can be understood today by checking the solutions for their stability. It is an interesting fact that stationary solutions are not always the most stable ones - this assumption might appear ``natural'', but is in fact quite misleading. To find out under which conditions one has to expect turbulence, we must have a closer look into the equations of hydrodynamics.
In a free flow (i.e. no outer confinements like tubes) and under sub-sonic conditions, one can treat air as an incompressible medium. This allows to use the Navier-Stokes equations (Navier 1827, extended by Stokes in 1845) which describe such a medium with viscosity (Eq. 9.2).
The respective terms describe:
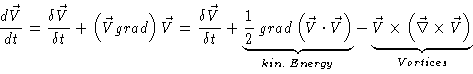 |
(9.3) |
Flow problems resemble each other for certain combinations of flow velocity, spatial dimension and viscosity. This allows to predict the general properties of a hydrodynamic system (and if it is turbulent or not) from small models or other well-studied cases where the geometries are the same. It is convenient to change to dimensionless equations by expressing lengths and velocities in units of the system's typical length scale l0 (e.g. the size of an obstacle) and the unperturbated flow velocity V0.
One obtains not only V'=V/V0 and l'=l/l0, but must change all other units
which are combinations of the two:
![]() ,
,
![]() and
and
![]() . As a result, we get the dimensionless equation
Eq.9.4:
. As a result, we get the dimensionless equation
Eq.9.4:
which contains Reynold's number
![]() . It
determines the relative influence of the energy dissipating term relative to the
non-linear turbulent term. A high Reynold's number will reduce the effect of
. It
determines the relative influence of the energy dissipating term relative to the
non-linear turbulent term. A high Reynold's number will reduce the effect of ![]() , so that turbulence will develop. Each problem has its specific Critical
Reynold's number Rec, which lies typically between 10 and 100. For a given
geometry and a Re>Rec, no stable solution exists (Fig.
, so that turbulence will develop. Each problem has its specific Critical
Reynold's number Rec, which lies typically between 10 and 100. For a given
geometry and a Re>Rec, no stable solution exists (Fig.![[*]](cross_ref_motif.gif) ).
).
With Eq.9.4 and the viscosities from Tab.9.1, we find that for
ambient conditions, wind moving faster than 1 cm/s hitting an obstacle bigger than
1 cm generates a turbulent flow. A house (10 m) in a 10 m/s wind has
![]() , mountains
, mountains
![]() .
.
This means that turbulence is something quite common in our environment. In our daily life, we encounter many turbulent systems which defy detailed prediction: leaves of wind-moved trees, eddies in flowing water, the structure of clouds, to name only a few. All these effects are non-linear and will never repeat themselves exactly, although their parameters stay within certain limits.
It may be surprising that these phenomena have been neglected by classical physics for centuries, to become finally popular in the wake of chaos theory and the development of powerful computers. One reason for this was surely the problem of repeating an experiment with inherent chaos exactly, and the sheer bulk of work for doing the calculations. Linear physics were favored not because they are more abundant in nature, but because they were easier to understand and reproduce.
Even chaos theory has a hard time with the atmosphere. The famous ``strange attractors'' which describe non-repetitive curves in solution spaces are not very useful for turbulence, because one is not sure if the number of solution space dimensions is finite or not in this case.
Meteorology is a well-known (and sometimes notorious) example for predictions of a non-linear system. In spite of a network of measurement stations and satellite data, boundary conditions are not known precisely enough for long term forecasts. This is the famous ``butterfly effect'': A butterfly moving its wings in South America may change the weather in Europe six months later.
But don't start hunting butterflys to prevent storms right now: this example only illustrates that non-linear systems do not obey the ``small cause - small effect'' rule of linear physics but a rather imprecise ``small cause at the right place may have a big effect'' rule. So it could be a butterfly, a spoken word, a thought, or a tree falling in a forest, or all of them together that may tip a balance.
For all practical applications, the interactions are too complex to backtrack the cause - but nevertheless, the history that makes a leaf move right now in a unique way outside your window contains somewhere the gravitational pull of faraway galaxies, and your mere presence will leave traces in the turbulent structures all over the universe (no liabilities implied, fortunately).
A small perturbation may set off a non-linear cause-and-effect chain, but this is only because a turbulent system can have multiple macroscopically different states without violating the conservation of energy. Using a statistical approach, we will now discuss turbulence's energy distribution on different scale sizes. This is an important step to understand how atmospheric parameters (including phase noise) change with time and distance.