

Next: 2.3 Delay Tracking and
Up: 2.2 The Heterodyne Interferometer
Previous: 2.2.1 Source Size Effects
Integrating over 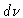 ,
,
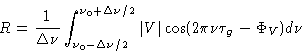 |
(2.18) |
Using
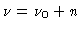
| R |
= |
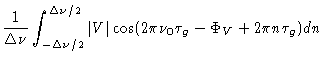 |
(2.19) |
| |
= |
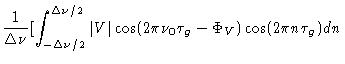 |
|
| |
|
![$\displaystyle - \int_{-\Delta \nu /2}^{\Delta \nu / 2}
\vert V\vert \sin(2 \pi \nu_0 \tau_g - \Phi_V) \sin(2 \pi n \tau_g) dn ]$](img220.gif) |
(2.20) |
| |
= |
![$\displaystyle \frac{1}{\Delta \nu} \vert V\vert \cos( 2 \pi \nu_0 \tau_g - \Phi...
... \pi n \tau_g) \right]_{-\Delta \nu /2}^{\Delta \nu / 2}
\frac{1}{2 \pi \tau_g}$](img221.gif) |
|
| |
|
![$\displaystyle + \frac{1}{\Delta \nu} \vert V\vert \sin( 2 \pi \nu_0 \tau_g - \P...
... \pi n \tau_g) \right]_{-\Delta \nu /2}^{\Delta \nu / 2}
\frac{1}{2 \pi \tau_g}$](img222.gif) |
(2.21) |
| |
= |
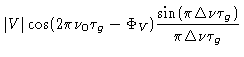 |
(2.22) |
The fringe visibility is attenuated by a
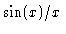 envelope,
called the bandwidth pattern, which falls off rapidly. A
1% loss in visibility is obtained for
envelope,
called the bandwidth pattern, which falls off rapidly. A
1% loss in visibility is obtained for
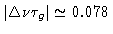 ,
or with
,
or with
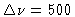 MHz and a baseline length b = 100m,
when the zenith angle
MHz and a baseline length b = 100m,
when the zenith angle 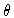 (defined in Fig.2.3) is 2 arcmin
only.
Thus, the ability to track a source for a significant hour angle
coverage requires proper compensation of the geometrical delay when a
finite bandwidth is desired.
(defined in Fig.2.3) is 2 arcmin
only.
Thus, the ability to track a source for a significant hour angle
coverage requires proper compensation of the geometrical delay when a
finite bandwidth is desired.



Next: 2.3 Delay Tracking and
Up: 2.2 The Heterodyne Interferometer
Previous: 2.2.1 Source Size Effects
S.Guilloteau
2000-01-19