



Next: 2.2.1 Source Size Effects
Up: 2. The interferometer principles
Previous: 2.1 Basic principle
Figure 2.2 is a schematic illustration of a 2-antenna
heterodyne interferometer.
Figure 2.2:
Schematic Diagram of a two-element interferometer
![\resizebox{12.0cm}{!}{\includegraphics[angle=270]{sg1f2.eps}}](img194.gif) |
Let us forget the frequency conversion for some time, i.e.
assume
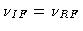 ...
...
The input (amplified) signals from 2 elements of the interferometer
are processed by a correlator, which is just a voltage multiplier followed
by a time integrator.
With one incident plane wave, the output r(t) is
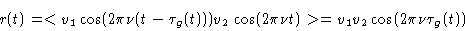 |
(2.11) |
where 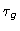 is obviously the geometrical delay,
is obviously the geometrical delay,
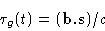 |
(2.12) |
As 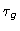 varies slowly because of Earth rotation, r(t) oscillates
as a cosine function, and is thus called the fringe pattern. As
we had shown before that v1 and v2 were proportional to the
electric field of the incident wave, the correlator output (fringe pattern)
is thus proportional to the power of the wave.
varies slowly because of Earth rotation, r(t) oscillates
as a cosine function, and is thus called the fringe pattern. As
we had shown before that v1 and v2 were proportional to the
electric field of the incident wave, the correlator output (fringe pattern)
is thus proportional to the power of the wave.




Next: 2.2.1 Source Size Effects
Up: 2. The interferometer principles
Previous: 2.1 Basic principle
S.Guilloteau
2000-01-19
![\resizebox{12.0cm}{!}{\includegraphics[angle=270]{sg1f2.eps}}](img194.gif)