



Next: 13.1.2 Fast Fourier Transform
Up: 13.1 Fourier Transform
Previous: 13.1 Fourier Transform
The simplest approach would be to directly compute 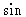 and
and 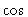 functions
in Eq.13.4 for all combinations of visibilities and pixels in the image.
This is straightforward, but slow. For typical data set from the VLA, which
contain up to 105 visibilities per hour and usually require large images
(
functions
in Eq.13.4 for all combinations of visibilities and pixels in the image.
This is straightforward, but slow. For typical data set from the VLA, which
contain up to 105 visibilities per hour and usually require large images
(
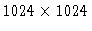 pixels), the computation time can be prohibitive. On the
other hand, the IRAM Plateau de Bure interferometer produces about 104 visibilities per synthesis,
and only require small images (
pixels), the computation time can be prohibitive. On the
other hand, the IRAM Plateau de Bure interferometer produces about 104 visibilities per synthesis,
and only require small images (
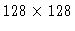 ). The Direct Fourier Transform
approach could actually be efficient on vector computers for spectral line data
from Plateau de Bure interferometer, because the
). The Direct Fourier Transform
approach could actually be efficient on vector computers for spectral line data
from Plateau de Bure interferometer, because the 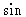 and
and 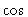 functions needs to be evaluated only
once for all channels. Moreover, the method is well suited to real-time display,
since the dirty image can be easily updated for each new visibility.
functions needs to be evaluated only
once for all channels. Moreover, the method is well suited to real-time display,
since the dirty image can be easily updated for each new visibility.




Next: 13.1.2 Fast Fourier Transform
Up: 13.1 Fourier Transform
Previous: 13.1 Fourier Transform
S.Guilloteau
2000-01-19