13. The Imaging Principles

Stéphane Guilloteau

IRAM, 300 rue de la Piscine, F-38406 Saint Martin d'Hères

You can also download a Compressed Postscript and a PDF version of this lecture
Assuming identical antennas, we have shown in previous lectures that an interferometer measures the visibility function

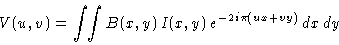$$V(u,v) = \ensuremath{\int\!\!\int} B(x,y)\, I(x,y)\, \ensuremath{e^{-2i\pi(ux+vy)}}\,dx\,dy$$ (13.1)

over an ensemble of points (u_i,v_i), i = 1,n, where B(x,y) is the power pattern of the antennas and I(x,y) the sky brightness distribution.

The imaging process consists in determining as best as possible the sky brightness I(x,y). Since Eq.13.1 is a convolution, the imaging process will involve deconvolution techniques.

Let S(u,v) be the sampling (or spectral sensitivity) function

 

$$S(u,v) \neq 0 \Longleftrightarrow \exists i \in 1,n \, (u_i,v_i) = (u,v)$$

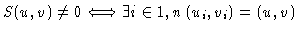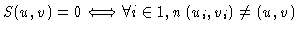$$S(u,v) = 0 \Longleftrightarrow \forall i \in 1,n \, (u_i,v_i) \neq (u,v)$$ (13.2)

The spectral sensitivity function S contains information on the relative weights of each visibility, usually derived from theoretical noise.

Let us define

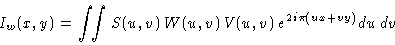$$I_w(x,y) = \ensuremath{\int\!\!\int} S(u,v)\, W(u,v)\, V(u,v)\, \ensuremath{e^{2i\pi(ux+vy)}}\,du\,dv$$ (13.3)

where W(u,v) is an arbitrary weighting function. Since the Fourier Transform of a product of two functions is the convolution of the Fourier Transforms of the functions, I_w(x,y) can be identified with

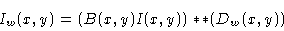$$I_w(x,y) = (B(x,y) I(x,y)) \ensuremath{\ast\!\ast} (D_w(x,y))$$ (13.4)

where

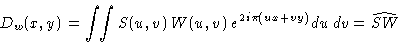$$D_w(x,y) = \ensuremath{\int\!\!\int} S(u,v)\, W(u,v)\, \ensuremath{e^{2i\pi(ux+vy)}}\,du\,dv = \widehat{S W}$$ (13.5)

D_w(x,y) is called the dirty beam, and is directly dependent on the choice of the weighting function W, as well as on the spectral sensitivity function S. I_w(x,y) is usually called the dirty image.

Fourier Transform, which allows to directly derive I_w from the measured visibilities V and spectral sensitivity function S, and Deconvolution, which allows to derive the sky brightness I from I_w, are thus two key issues in imaging (see Eq.13.4).