Two kinds of charged particles can exist in a superconductor:
a) ordinary electrons; b) so-called Cooper pairs, consisting of two
electrons interacting and weakly bound together by the exchange of
phonons (lattice vibrations); breaking a Cooper pair costs an energy
![]() . Correspondingly, two kinds of currents can
flow across the junction: the Josephson current, consisting of Cooper
pairs, and the so-called quasi-particle current, consisting of
``ordinary'' electrons (presumably ``electron'' did not sound fancy
enough). To keep this digression into SIS physics short, let's just
state that the Josephson current can be ignored. At the operating
temperature of the mixer, and in an unbiased junction, the population of
quasi-particles is virtually negligible. But, if the bias voltage is
raised to the gap voltage
. Correspondingly, two kinds of currents can
flow across the junction: the Josephson current, consisting of Cooper
pairs, and the so-called quasi-particle current, consisting of
``ordinary'' electrons (presumably ``electron'' did not sound fancy
enough). To keep this digression into SIS physics short, let's just
state that the Josephson current can be ignored. At the operating
temperature of the mixer, and in an unbiased junction, the population of
quasi-particles is virtually negligible. But, if the bias voltage is
raised to the gap voltage
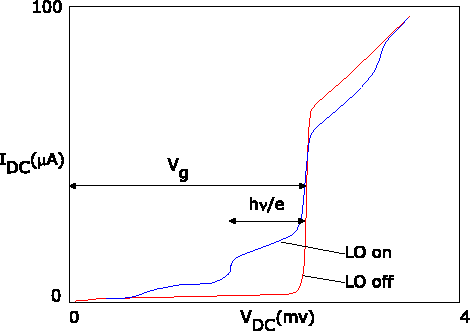 |
In the presence of electromagnetic radiation, the situation is modified
as follows. If a RF photon is absorbed, its energy ![]() can contribute
to the energetic budget, which can now be written as:
can contribute
to the energetic budget, which can now be written as:
So far I have shown you qualitatively that an SIS junction can function as
a total power detector. The responsivity (current generated per power
absorbed) can even be estimated to be of the order of one electron per
photon, or:
![]() . How does that relate to frequency
downconversion? Assume that a power detector is fed the sum of a local
oscillator (normalized to unit amplitude for convenience)
. How does that relate to frequency
downconversion? Assume that a power detector is fed the sum of a local
oscillator (normalized to unit amplitude for convenience)
![]() and a much smaller signal at a
nearby frequency:
and a much smaller signal at a
nearby frequency:
![]() . Assumes this functions
as a squaring device and discard high-frequency terms in the output:
. Assumes this functions
as a squaring device and discard high-frequency terms in the output:
The LO power requirement for an SIS mixer can be estimated as follows. A voltage
scale is defined by the width of the photon step: ![]() . Likewise, a resistance
scale can be defined from RN, the resistance of the junction above Vg;
junctions used in mixers have
. Likewise, a resistance
scale can be defined from RN, the resistance of the junction above Vg;
junctions used in mixers have
![]() . So, the order of magnitude of
the LO power required is:
. So, the order of magnitude of
the LO power required is:
Because the insulating barrier of the junction is so thin, it possesses a
capacitance of about
![]() . At the RF and LO frequencies, the
(imaginary) admittance of that capacitance is about 3-4
. At the RF and LO frequencies, the
(imaginary) admittance of that capacitance is about 3-4![]() the
(approximately real) admittance of the SIS junction itself. Therefore,
appropriate tuning structures must be implemented to achieve a good
impedance match (i.e. energy coupling) of the junction to the signals.
the
(approximately real) admittance of the SIS junction itself. Therefore,
appropriate tuning structures must be implemented to achieve a good
impedance match (i.e. energy coupling) of the junction to the signals.
The minimum theoretical SSB noise for an SIS mixer is ![]() , 11K at 230GHz;
the best IRAM mixers come within a factor of a few (
, 11K at 230GHz;
the best IRAM mixers come within a factor of a few (
![]() ) of that
fundamental limit. These numbers are for laboratory measurements with minimal optics
losses; practical receivers have a slightly higher noise.
) of that
fundamental limit. These numbers are for laboratory measurements with minimal optics
losses; practical receivers have a slightly higher noise.