



Next: 4.2 Basic Theory
Up: 4. Cross Correlators
Previous: 4. Cross Correlators
As we already learned in the lecture on radio interferometry
by S.Guilloteau (Chapter 2),
the interferometer measures the complex cross-correlation
function of the voltage at the outputs of a pair of antennas (i,j).
This quantity,
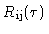 is defined as
is defined as
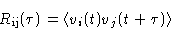 |
(4.1) |
(the brackets indicate the time average, see AppendixA).
The cross-correlation function is related to the visibility function
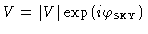 by
by
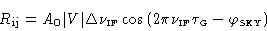 |
(4.2) |
where A0 is the collecting area of the antenna.
Eq.4.2 only holds for a quasi-monochromatic signal,
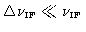 (.e. the bandpass may be
represented by a
(.e. the bandpass may be
represented by a 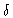 -function).
The signal phase varies with time due to source structure and atmospheric
perturbations (expressed by
-function).
The signal phase varies with time due to source structure and atmospheric
perturbations (expressed by
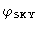 ), and due to the geometric delay
), and due to the geometric delay
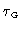 . The timescale that is needed to fully sample a spectral line,
given by the sampling theorem (see below) is much shorter. Here are examples
of the different timescales:
. The timescale that is needed to fully sample a spectral line,
given by the sampling theorem (see below) is much shorter. Here are examples
of the different timescales:
- 1.
- timescale for phase variation by
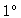 due to source structure
(for a point source at 98GHz with
due to source structure
(for a point source at 98GHz with
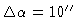 offset from
phase reference center, east-west baseline of 258m during transit):
2min
offset from
phase reference center, east-west baseline of 258m during transit):
2min
- 2.
- timescale for phase variation due to atmospheric perturbations:
(depending on atmospheric conditions and baseline length):
1sec - several hours
- 3.
- sampling time step for a 80 MHz bandwidth:
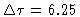 ns
ns
- 4.
- maximum time lag needed for a 40 kHz resolution
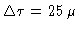 s
s
In the following, I will discuss digital techniques to evaluate
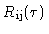 . Analog methods of signal processing are highly
impractical in radio interferometry, for mainly two reasons:
. Analog methods of signal processing are highly
impractical in radio interferometry, for mainly two reasons:
- 1.
- In time domain, high precision is needed.
- 2.
- The signal needs to be identically copied, in order to cross-correlate
the output of one antenna with the outputs from all other antennas.
This can be more easily done with digital techniques, than with analog ones.
The first signal processing steps are analog, beginning with the
mixing in the heterodyne receivers.
For reasons that will become clear later (see R.Lucas, Chapter 5),
only the case of single-sideband reception is considered.
The sidebands may be separated by a periodic phase shift of 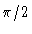 applied to the local oscillator. The signals are demodulated in two different
ways by the correlator. At the entry of the correlator, filters
are inserted, that are used to select the intermediate frequency
bandpass. The following signal processing steps are
digitally implemented, and are performed within the correlator:
applied to the local oscillator. The signals are demodulated in two different
ways by the correlator. At the entry of the correlator, filters
are inserted, that are used to select the intermediate frequency
bandpass. The following signal processing steps are
digitally implemented, and are performed within the correlator:
- 1.
- Sampling the signal: in order to digitize the signal, it needs
to be sampled. Bandwidth-limited signals (i.e. containing frequencies between
zero and
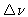 )
may be sampled without loss of interformation if the
samples are taken at time intervals
)
may be sampled without loss of interformation if the
samples are taken at time intervals
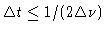 .
.
- 2.
- In order to numerically compute the cross correlation function, the
signals have to be discretized. The data are affected by such a quantization,
but may be corrected for it. However, the loss of information cannot be
recovered and degrades the correlator sensitivity.
- 3.
- Delay compensation: the geometric delays are eliminated for signals
received from the direction of the pointing center. Remaining delays are
due to source structure.
- 4.
- Until now, everything is done in the time domain. However, for
spectroscopic applications, the desired output is the cross power spectral
density, and not the cross correlation function. These quantities are
Fourier-transform pairs (Wiener-Khintchine theorem). The
transformation can be efficiently done by a processor performing a
Fast Fourier Transform.
The plan of this lecture is as follows: after the basic theory, I will talk
about the correlator in practice. Both intrinsic limitations, and
system-dependent performance will be discussed.
For further reading, the book of [Thompson et al 1986] (chapters 6 - 8),
and the introduction by [D'Addario 1989] are recommended. Finally, as an
example, the current correlator system on Plateau de Bure, and its upgrade in
the near future, will be presented.
Figure 4.1:
Architecture
of a complex continuum cross correlator.
![\resizebox{\hsize}{!}{\includegraphics[angle=270]{hwfig1.eps}}](img344.gif) |
Figure 4.2:
Architecture
of a complex spectroscopic cross correlator.
![\resizebox{\hsize}{!}{\includegraphics[angle=270]{hwfig2.eps}}](img345.gif) |




Next: 4.2 Basic Theory
Up: 4. Cross Correlators
Previous: 4. Cross Correlators
S.Guilloteau
2000-01-19
![]() . Analog methods of signal processing are highly
impractical in radio interferometry, for mainly two reasons:
. Analog methods of signal processing are highly
impractical in radio interferometry, for mainly two reasons: