



Next: 1.3 The perfect Single-Dish
Up: 1. Radio Antennas
Previous: 1.1 Introduction
The properties of electromagnetic radiation propagation and of radio antennas
can be deduced from a few basic physical principles, i.e.
- 1.
- the notion that Electromagnetic Radiation are Waves of a certain
Wavelength (
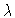 ), or Frequency (
), or Frequency (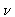 ), and Amplitude (A) and Phase (
), and Amplitude (A) and Phase (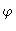 );
);
- 2.
- from Huygens Principle which says that each element of a wavefront is the
origin of a Secondary Spherical Wavelet;
- 3.
- the notion that the Optical Instrument (like a single-dish antenna, a
telescope, etc.) combined with a receiver manipulates the incident wavefront
through their respective phase and amplitude transfer functions.
Figure 1.1:
Illustration
of Huygens Principle. The individual points of the plane wavefront in the aperture
plane are the origin of secondary spherical wavelets, which propagate to
the right, and superpose to form a plane wavefront in the image plane.
The optical instrument is placed in between.
![\resizebox{8cm}{!}{\includegraphics[angle=270.0]{greve1.eps}}](img59.gif) |
Summarized in one sentence, and proven in the following, we may say that the radio
antenna transforms the radiation incident on the aperture plane (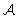 ) to an
image in the image plane (
) to an
image in the image plane (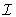 ), also called focal plane. Following Huygens
Principle illustrated in Figure 1.1, the point a(x,y)
), also called focal plane. Following Huygens
Principle illustrated in Figure 1.1, the point a(x,y) 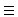 a(
a(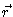 )
of the incident wavefront in the aperture plane
)
of the incident wavefront in the aperture plane 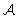 is the origin of a
spherical wavelet of which the field
is the origin of a
spherical wavelet of which the field 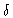 E(a') at the point a'(u,v)
E(a') at the point a'(u,v)
 a(
a( ) in the image plane
) in the image plane  is
is
![\begin{displaymath}{\delta}{\rm E}({\vec u}) = {\rm A}({\vec r}){\rm exp[iks]/s}
\end{displaymath}](img66.gif) |
(1.1) |
with k = 2
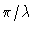 . The ensemble of spherical wavelets arriving from all
points of
. The ensemble of spherical wavelets arriving from all
points of 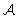 at the point a
at the point a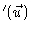 of the image plane
of the image plane 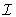 produces
the field
produces
the field
![\begin{displaymath}{\rm E}({\vec u}) = {\int}_{{\cal A}}{\rm A}({\vec r}){\Lambda}({\beta}) [{\rm
exp(iks)/s}] dx dy
\end{displaymath}](img69.gif) |
(1.2) |
For the paraxial case, when the rays are not strongly inclined against the
direction of wave propagation (i.e. the optical axis), the inclination
factor 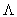 can be neglected since
can be neglected since 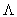 (
(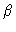 )
) 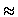 cos(
cos(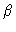 )
) 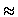 1. Also, s
1. Also, s 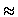 s0 for paraxial rays, but
exp[iks]
s0 for paraxial rays, but
exp[iks] 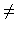 exp[iks0] since these are cosine and sine terms of s
where a small change in s may produce a large change of the cosine or sine
value. Thus, for the paraxial approximation we may write
exp[iks0] since these are cosine and sine terms of s
where a small change in s may produce a large change of the cosine or sine
value. Thus, for the paraxial approximation we may write
![\begin{displaymath}s = [{\rm (x-u)}^2 + {\rm (y-v)}^2 + {\rm z}^2]^{1/2}\ \approx\ {\rm R + g(x,y,R) -
(xu + yv)/R}
\end{displaymath}](img73.gif) |
(1.3) |
with
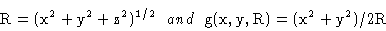 |
(1.4) |
When using these expressions in Eq.1.2, we obtain
![\begin{displaymath}{\rm E(u,v) = [exp(ikR)/s}_{0}]{\int}_{{\cal A}}{\rm A(x,y)} {\rm exp[ik(g(x,y,R) -
(ux + vy)/R)] dx dy}
\end{displaymath}](img75.gif) |
(1.5) |
This equation describes the paraxial propagation of a wavefront, for instance
the wavefront arriving from a very far away star. In particular, this equation
says, that without disturbances or manipulations in between  and
and  the plane wavefront continues to propagate in straight direction as a plane
wavefront.
the plane wavefront continues to propagate in straight direction as a plane
wavefront.




Next: 1.3 The perfect Single-Dish
Up: 1. Radio Antennas
Previous: 1.1 Introduction
S.Guilloteau
2000-01-19
![\resizebox{8cm}{!}{\includegraphics[angle=270.0]{greve1.eps}}](img59.gif)
![]() ) to an
image in the image plane (
) to an
image in the image plane (![]() ), also called focal plane. Following Huygens
Principle illustrated in Figure 1.1, the point a(x,y)
), also called focal plane. Following Huygens
Principle illustrated in Figure 1.1, the point a(x,y) ![]() a(
a(![]() )
of the incident wavefront in the aperture plane
)
of the incident wavefront in the aperture plane ![]() is the origin of a
spherical wavelet of which the field
is the origin of a
spherical wavelet of which the field ![]() E(a') at the point a'(u,v)
E(a') at the point a'(u,v)
![]() a(
a(![]() ) in the image plane
) in the image plane ![]() is
is