5.1.1 The simple interferometer

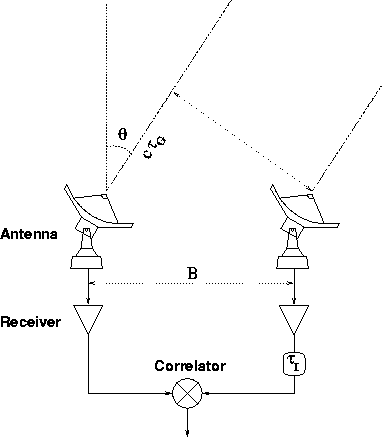
This is composed of 2 antennas, a multiplier, an integrator (Fig. 5.1); we directly multiply the signals, and average in time. 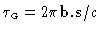$\ensuremath{\tau_\mathrm{\scriptscriptstyle G}} = 2\pi \ensuremath{\mathbf b} . \ensuremath{\mathbf s} /c$ is the geometrical delay.

  

Figure 5.1: A simple, two-antenna interferometer

Provided the geometrical delay is compensated in the hardware, after filtering out the high frequency terms, the output of the correlator is the real part of the visibility:

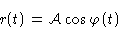$$r(t) = \ensuremath{\mathcal{A}} {} \cos{\ensuremath{\varphi_\mathrm{\scriptscriptstyle }} (t)}$$ (5.1)

A complex correlator using a quadrature network can be used to mesure the imaginary part; or (equivalently) one uses a spectral correlator.