There is still a free parameter in the image construction process: the weighting
function. At ![]() table creation, the sampling function is defined as
table creation, the sampling function is defined as
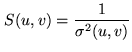 |
(15.25) |
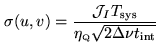 |
(15.26) |
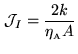 |
(15.27) |
The weights ![]() can be freely chosen. The selecting of weights is usually decomposed
in two slightly different processes, called Weighting and Tapering.
can be freely chosen. The selecting of weights is usually decomposed
in two slightly different processes, called Weighting and Tapering.
Weighting deals with the local variations of weights for each grid cell after
the gridding process. Since the original ![]() coverage is an ensemble of ellipses,
the gridding may leave a weight distribution with very large dispersion. Weighting
can be applied to uniformize this distribution.
coverage is an ensemble of ellipses,
the gridding may leave a weight distribution with very large dispersion. Weighting
can be applied to uniformize this distribution.
On the other hand, Tapering consists in apodizing the ![]() coverage by
coverage by
![]() where
where ![]() is a tapering distance. This corresponds to
smoothing the data in the map plane (by convolution with a gaussian).
is a tapering distance. This corresponds to
smoothing the data in the map plane (by convolution with a gaussian).
The simplest possibility, called Natural Weighting, without taper is
to keep the original spectral sensitivity function by setting
![]() .
This can be demonstrated to maximize sensitivity to point sources (i.e.
sources smaller than the synthesized beam). Proper design (and use) of the array can ensure
that the resulting synthesized beam is appropriate, in terms of size (angular resolution
matched to the scientific goal) and shape (lowest possible sidelobes).
.
This can be demonstrated to maximize sensitivity to point sources (i.e.
sources smaller than the synthesized beam). Proper design (and use) of the array can ensure
that the resulting synthesized beam is appropriate, in terms of size (angular resolution
matched to the scientific goal) and shape (lowest possible sidelobes).
If the sources of interest are somewhat extended, tapering can be used to increase
brightness sensitivity. Tapering may also have the advantage of lowering the
sidelobes. This is usually true for limited tapering, which reduces the effect of
the discontinuity at the outer edge of the ![]() plane, but is not the case for
strong tapering, where the result becomes critically dependent on the actual
sampling of the inner part of the
plane, but is not the case for
strong tapering, where the result becomes critically dependent on the actual
sampling of the inner part of the ![]() plane. However, tapering is always throwing
out some information, namely the long baselines part of the data set. Hence, it
should be used either with moderate tapers, or as a complementary view on a data
set. To increase brightness sensitivity, one should use preferentially compact
arrays rather than tapering.
plane. However, tapering is always throwing
out some information, namely the long baselines part of the data set. Hence, it
should be used either with moderate tapers, or as a complementary view on a data
set. To increase brightness sensitivity, one should use preferentially compact
arrays rather than tapering.
Uniform Weighting consists in selecting the weights ![]() so that the sum of weights
so that the sum of weights
![]() over a
over a ![]() cell is a constant function
(or zero if no
cell is a constant function
(or zero if no ![]() data exists in that cell). The size (radius) of the
data exists in that cell). The size (radius) of the ![]() cell
is an arbitrary parameter. It can be the cell size resulting from the gridding
process, i.e. the inverse of the field of view, but any other choice is possible.
Using half of the dish diameter is well justified, since the visibilities are
convolution of Fourier transform of the sky brightness by the Fourier transform of
the primary beam. Uniform Weighting gives more weight to long baselines than
natural weighting (because you spend less time per
cell
is an arbitrary parameter. It can be the cell size resulting from the gridding
process, i.e. the inverse of the field of view, but any other choice is possible.
Using half of the dish diameter is well justified, since the visibilities are
convolution of Fourier transform of the sky brightness by the Fourier transform of
the primary beam. Uniform Weighting gives more weight to long baselines than
natural weighting (because you spend less time per ![]() cell on long baselines than
on short baselines for earth synthesis). Uniform Weighting produces smaller
beam. Because it fills the
cell on long baselines than
on short baselines for earth synthesis). Uniform Weighting produces smaller
beam. Because it fills the ![]() plane more regularly, Uniform weighting could be
thought also to produce lower sidelobes. However, because of the discontinuity of
the weights at the edge of the sampled portion of the
plane more regularly, Uniform weighting could be
thought also to produce lower sidelobes. However, because of the discontinuity of
the weights at the edge of the sampled portion of the ![]() plane, the inner
sidelobes tend to be increased, unless some tapering is combined with Uniform
weighting.
plane, the inner
sidelobes tend to be increased, unless some tapering is combined with Uniform
weighting.
Robust Weighting is a variant of uniform weighting which avoids to give too
much weight to a ![]() cell with low natural weight. There are several ways to
implement such a scheme. Roughly speaking, if the sum of natural weights in a cell
is less than a threshold, the weighting is unchanged, if it is more, the weight is
set to this threshold. Let
cell with low natural weight. There are several ways to
implement such a scheme. Roughly speaking, if the sum of natural weights in a cell
is less than a threshold, the weighting is unchanged, if it is more, the weight is
set to this threshold. Let ![]() be the natural weight of a cell, and
be the natural weight of a cell, and ![]() a
threshold for such weight. Robust weighting could be implemented by selecting the
weight W as
a
threshold for such weight. Robust weighting could be implemented by selecting the
weight W as
| (15.28) |
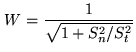 |
(15.29) |
Robust weighting combines the advantages of Natural and
Uniform weighting, by increasing the resolution and lowering the
sidelobes without degrading too much the sensitivity. By adjusting the threshold, it approaches either case (large threshold
![]() Natural,
small threshold
Natural,
small threshold
![]() Uniform).
Uniform).
Weighting and Tapering reduce point source sensitivity by
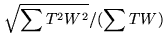 |
(15.30) |