19.2 Spectral Line Sources

Unfortunately, things get even worse for spectral lines, because the uncertainties on the line width and source velocity add up to the position and size problem. If the source velocity is unknown, the observer will tend to select the brightest part of the spectrum to define the integrated flux. This result in a positive bias on the flux. Furthermore, if the line width is not known, the observe may limit the line to the brightest part of the spectrum, resulting in another bias. This bias is in general positive, since positive noise peaks will be included in the line region, but could be negative for specific line shapes.

If the source position was a priori unknown, it is common practice to determine it from the integrated line flux map made using the tailored line window specified by the astronomer. Such a procedure results in a positively biased total flux. Any speculated extension will also increase the total flux, by enlarging the selected image region by selection of positive noise peaks. The net effect is a 1 to 2 $\sigma$ positive bias on the integrated line flux. Things get really messy if a continuum is superposed to the weak line...

A good strategy is required to minimize these biases. The correct approach to point sources (or sources less than about $1/3^{\mathrm{rd}}$ of the synthesized beam), is to first determine the position (e.g. from continuum data is available, or from the integrated line map if not, or ideally from other data). Once the position is fixed, the line profile can be derived by fitting a point (or small fixed size) source, at fixed position into the $UV$ data. Using this line profile, the total line flux, as well as source velocity and line width, can be derived by fitting an appropriate lineshape, e.g. a Gaussian if no other information is available. In this last step, a constant baseline offset should be added if there is a continuum contribution.

For extended sources, which may be affected by velocity gradient, one has to fit a multi-parameter (6 for an elliptical gaussian) source model for each spectral channel into the $UV$ data. As a consequence, the signal in each channel should be at least $6 \sigma$ to derive any meaningful information. The strict minimum is $4 \sigma$ (per line channel...) to get flux and position for a fixed size source. Velocity gradients are not believable unless even better signal to noise is obtained per line channel !...Moreover, for narrow lines, most correlators produce spectral channels which are not independent; the correlation between adjacent channels should be taken into account when analyzing velocity gradients.

To sum up the weak spectral line problems:

• Do not believe velocity gradient unless proven at a 5 $\sigma$ level. This requires a S/N larger than 6 in each channel. Remember that position accuracy per channel is the beamwidth divided by the signal-to-noise ratio...
• Do not believe source size unless $S/N > 10$ (or better)
• Expect line widths to be very inaccurate
• Expect integrated line intensity to be positively biased by 1 to 2 $\sigma$
• or even more biased if the source is extended

These biases are the analogous of the Malmquist bias.

Unfortunately, examples for such problems are numerous, especially for high redshift CO lines. The $z=2.8$ galaxy 53W002 was detected in CO with the OVRO interferometer by [Scoville et al 1997], who claim an extended source, with velocity gradient. The published images (contour maps) look convincing, but this is biased by the chosen visual representation, with contours starting at $2 \sigma$ but spaced by $1 \sigma$. This creates the visual impression of higher S/N ratio. The published spectra also looks convincing, but are presented as a fully sampled spectra (i.e. channel width equal to twice the channel separation). Although this is the proper way to present a complete information, the astronomer's eye is not accustomed to such a presentation, and the astronomer tends to interpret the data as if the channels were independent, thereby underestimating the noise. Yet the total line flux is $1.5 \pm 0.2$ Jy.km/s i.e. (at best) only 7 $\sigma$, and thus, according to the discussion presented above, no extension/gradient should be measurable. Indeed, using the IRAM interferometer, [Alloin et al 2000] find a line flux of $1.20 \pm 0.15$ Jy.km/s, no source extension, no velocity gradient, different line width and redshift. Note that the line fluxes agree within the errors, with the second determination just $1 \sigma$ below the first one, as expected for an initially biased result...

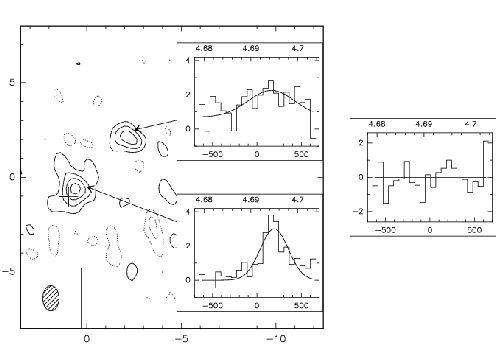
Another example of visually misleading result is shown in Fig.19.2. Although the two spectra appear different, there is a weak continuum (which was measured independently) on the Northern source. Once the continuum offset and a scale factor have been applied, the lack of visible structure in the difference spectrum shows that both line profiles are indistinguishable, i.e. that there is no measurable velocity gradient. These two sources could be lensed images of the same galaxy...

Figure 19.2: Example of search for a Velocity Gradient: BR 1202-0725. The image is a contour map of dust emission at 1.3 mm, with 2 $\sigma$ contours. The inserts are redshifted CO(5-4) spectra from the indicated directions. A weak continuum (measured independently) exist on the Northern source. The rightmost insert is a difference spectrum (with a scale factor applied, and continuum offset removed) (Cox, Guélin, Guilloteau & Omont, in preparation).