5.3 Why we need heterodyne receivers

In the present context, heterodyne refers to receivers where the frequency of the input signal is shifted to lower frequencies. This is done by adding to the (small) input signal a (relatively) strong monochromatic signal, called the local oscillator (LO) and passing the sum through a non-linear device, whose output contains (among others) the difference frequency. Although a non-linear device is involved, the transformation from input to output is linear for the small signal. This process is called mixing or down-conversion. The output signal is called the intermediate frequency (IF). Actually the complete signal processing at a radiotelescope can involve up to four heterodyne conversions. The process of mixing is illustrated by figure 5.4 and by the simple equations below.

$$v_{LO} = V_{LO} \cos(\omega_{LO}t)$$

$$v_{S} = V_{S} \cos(\omega_{S}t+\phi_S)$$

$$v_{IF} = A (v_{LO}+v_{S})^2$$

$$= A V_{LO}V_{S}\cos((\omega_{S}-\omega_{LO})t+\phi_S)+\cdots$$

$$= A V_{LO}V_{S}\cos((\omega_{LO}-\omega_{S})t-\phi_S)+\cdots$$

Interferometric observers, take a look at the last two lines, and note that, if you insist on keeping positive angular frequencies (and you really should), the signal phase enters in the IF phase with a positive sign in USB ( $\omega_{S}>\omega_{LO}$), and a negative side in LSB.

Figure 5.4: Frequency down-conversion by mixing. Left: schematic diagram. Right: representation in frequency space.

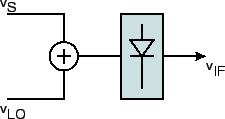
The first reason why heterodyne down-conversion is needed is that only few signal processing devices exist at millimeter frequencies, and definitely not the fully parallel spectrometers (as opposed to multiplex devices such as FTS) that are routinely used for spectroscopic observations.

Then arises the question of where in the signal processing chain to operate the down-conversion. Basically we have no choice, because hardly any amplifiers are available in the millimeter range, except in the 3mm band, where they do not match the low noise properties of SIS mixers (to be discussed below). So we must perform a down-conversion before we can amplify the signal.

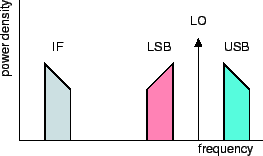
Before we leave the topic, it is worth noting that heterodyne means different things to different people. For engineers, it means that a mixer is used for down-converting the signal frequency; that's how the word is used above. For astronomers, heterodyne receivers are associated with spectroscopic observations; yet, there is only a quantitative difference, but no essential difference, between bolometer detection with a 80-GHz bandpass, and observing with a filterbank having 1-MHz bandpass. Finally, for physicists, heterodyne means with phase-preserving. In that sense, indeed, a bolometer is not phase-preserving, while a ``heterodyne'' receiver is phase-preserving only if it is defined without the final detector.