



Next: 6.4 The correlator on
Up: 6. Cross Correlators
Previous: 6.2 Basic Theory
Contents
Subsections
In order to numerically evaluate the cross-correlation function
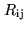 ,
the continuous signals entering the cross correlator need
to be sampled and quantized.
According to Shannon's sampling theorem [Shannon 1949], a
bandwidth-limited signal may be entirely recovered by sampling it at time
intervals
,
the continuous signals entering the cross correlator need
to be sampled and quantized.
According to Shannon's sampling theorem [Shannon 1949], a
bandwidth-limited signal may be entirely recovered by sampling it at time
intervals
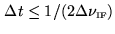 (also called sampling at
Nyquist rate). The discrete Fourier transform of the sufficiently sampled
cross-correlation function theoretically yields the cross-power spectrum
without loss of information. However, in practice, two intrinsic limitations
exist:
(also called sampling at
Nyquist rate). The discrete Fourier transform of the sufficiently sampled
cross-correlation function theoretically yields the cross-power spectrum
without loss of information. However, in practice, two intrinsic limitations
exist:
- In order to discretize a signal, it is not only sampled, it also
has to be quantized. The cross-correlation function, as
derived from quantized signals, does not equal the cross-correlation function
of continuous signals. Moreover, the sampling theorem does not hold anymore for
quantized signals. The reasons will become clear below.
- Eq.6.7 theoretically extends from
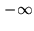 to
to 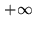 .
In practice (Eq.6.8), only a maximum time lag can be considered: limited storage
capacities and digital processing speed are evident reasons, another limiting
factor are the different timescales mentioned before.
The abrupt cutoff of the time window affects the data.
.
In practice (Eq.6.8), only a maximum time lag can be considered: limited storage
capacities and digital processing speed are evident reasons, another limiting
factor are the different timescales mentioned before.
The abrupt cutoff of the time window affects the data.
These ``intrinsic'' limitations are discussed in Sections 6.3.1 and 6.3.2.
The system-dependent performance will be addressed in Section 6.3.3.
6.3.1 Digitization of the input signal and clipping correction
As already mentioned, sampling at the Nyquist rate retains all information.
However, quantizing the input signal leads to a loss of information.
This can be qualitatively understood in the following way:
in order to reach the next discrete level of the transfer function,
some offset has to be added to the signal. If the input signal is random noise
of zero mean, the offset to be added will also be a random signal of zero mean.
In other words, a ``quantization'' noise is added to the signal, that leads to
a loss of information. In addition, the added noise is not anymore bandwidth
limited, and the sampling theorem does not apply: oversampling will lead
to improved sensitivity.
Many quantization schemes exist (see e.g. [Cooper 1970]). It is
entirely sufficient to use merely a few quantum steps, if the
cross-correlation function will be later corrected for the effects
of quantization. For the sake of illustration, the transfer
function of a four-level 2-bit quantization is shown in
Fig.6.5. Each of the four steps is assigned a
sign bit, and a magnitude bit. After discretizing the signal, the
samples from one antenna are shifted in time, in order to
compensate the geometric delay
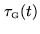 . The correlator
now proceeds in the following way: for each delay step
. The correlator
now proceeds in the following way: for each delay step 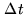 ,
the corresponding sign and magnitude bits are put into two
registers (one for the first antenna, and one for the second). The
second register is successively shifted by one sample. In this
way, sample pairs from both antennas, separated by a successively
longer time lag, are created. These pairs are multiplied, using a
multiplication table. For the case of four-level quantization, it
is shown in Fig.6.5. Products which are assigned
a value of
,
the corresponding sign and magnitude bits are put into two
registers (one for the first antenna, and one for the second). The
second register is successively shifted by one sample. In this
way, sample pairs from both antennas, separated by a successively
longer time lag, are created. These pairs are multiplied, using a
multiplication table. For the case of four-level quantization, it
is shown in Fig.6.5. Products which are assigned
a value of 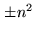 are called ``high-level products'', those
with a value of
are called ``high-level products'', those
with a value of 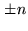 are ``intermediate-level products'', and
those with a value of
are ``intermediate-level products'', and
those with a value of 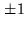 ``low-level products''. The
products (evaluated using the multiplication table in
Fig.6.5) are sent to a counter (one counter for
each channel, i.e. for each of the discrete time lags). After the
end of the integration cycle, the counters are read out.
``low-level products''. The
products (evaluated using the multiplication table in
Fig.6.5) are sent to a counter (one counter for
each channel, i.e. for each of the discrete time lags). After the
end of the integration cycle, the counters are read out.
In practice, the multiplication table will be shifted by a
positive offset of 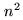 , to avoid negative products (the offset
needs to be corrected when the counters are read out). This is
because the counter is simply an adding device. As another
simplification, low-level products may be deleted. This makes
digital implementation easier, and accounts for a loss of
sensitivity of merely 1% (see Table 6.1). Finally,
not all bits of the counters' content need to be transmitted (see
Section 6.3.2).
, to avoid negative products (the offset
needs to be corrected when the counters are read out). This is
because the counter is simply an adding device. As another
simplification, low-level products may be deleted. This makes
digital implementation easier, and accounts for a loss of
sensitivity of merely 1% (see Table 6.1). Finally,
not all bits of the counters' content need to be transmitted (see
Section 6.3.2).
Before the normalized contents of the counters are Fourier-transformed,
they need to be corrected, because the cross-correlation function of
quantized data does not equal the cross-correlation function of continuous
data. This ``clipping correction'' can be derived using two different
methods. As an example for the case of full 4-level quantization:
- Four-level cross-correlation coefficient according to the multiplication
table Fig.6.5. The cross-correlation coefficient
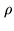 is a normalized form of the cross-correlation function (see
AppendixA):
is a normalized form of the cross-correlation function (see
AppendixA):
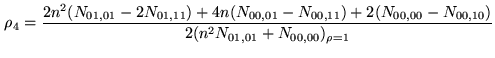 |
(6.8) |
where
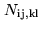 is the number of counts with sign bit
is the number of counts with sign bit 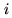 and magnitude
bit
and magnitude
bit 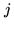 at time
at time 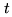 (first antenna), and sign bit
(first antenna), and sign bit 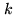 and magnitude bit
and magnitude bit 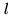 at
time
at
time 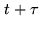 (second antenna).
(second antenna). 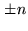 is the product value assigned to
intermediate-level products.
is the product value assigned to
intermediate-level products.
- Clipping correction, first method: evaluate the
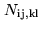 in
Eq.6.9, using joint probabilities
in
Eq.6.9, using joint probabilities
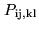 (see AppendixA
for the definition of the jointly Gaussian probability distribution), such as
(see AppendixA
for the definition of the jointly Gaussian probability distribution), such as
![$\displaystyle N_{01,01} = NP_{01,01} = \frac{N}{2\pi\sigma^2\sqrt{1-\rho^2}} \i...
...nfty}{ \exp{\left[\frac{-(x^2+y^2-2\rho xy)}{2\sigma^2(1-\rho^2)}\right]}dx}dy}$](img698.png) |
(6.9) |
(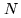 is the number of signal pairs, separated by the time lag of the channel
under consideration,
is the number of signal pairs, separated by the time lag of the channel
under consideration, 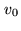 is the clipping voltage, see Fig.6.4).
is the clipping voltage, see Fig.6.4).
- Clipping correction, second method: using Price's theorem for functions
of jointly random variables. The result, derived in AppendixB, is shown in
Fig.6.4:
Although the discrete, normalized cross-correlation function and the
continuous cross-correlation coefficient are almost linearly dependent within
a wide range, the correction is not trivial. An analytical solution is only
possible for the case of two-level quantization (``van Vleck correction''
[Van Vleck 1966]).
In practice, several methods are used to numerically implement
Eq.6.11 (in the following, the index 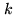 means
k-level quantization). The integrand may be replaced by an interpolating
polynomial, allowing to solve the integral. One may also construct
an interpolating surface
means
k-level quantization). The integrand may be replaced by an interpolating
polynomial, allowing to solve the integral. One may also construct
an interpolating surface
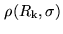 . As already discussed, the
clipping correction cannot recover the loss of sensitivity due to
quantization. The loss of sensitivity for
. As already discussed, the
clipping correction cannot recover the loss of sensitivity due to
quantization. The loss of sensitivity for 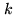 -level discretization may be
found by evaluating the signal-to-noise ratio
-level discretization may be
found by evaluating the signal-to-noise ratio
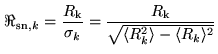 |
(6.11) |
In order to minimize the loss of sensitivity, the clipping voltage (with
respect to the noise 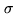 ) needs to be adjusted such that the
correlator efficiency curve in Fig.6.4 is at its maximum.
The correlator efficiency is defined with respect to the signal-to-noise
ratio of a (fictive) continuous correlator, i.e.
) needs to be adjusted such that the
correlator efficiency curve in Fig.6.4 is at its maximum.
The correlator efficiency is defined with respect to the signal-to-noise
ratio of a (fictive) continuous correlator, i.e.
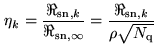 |
(6.12) |
where 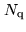 is the number of samples. Table6.1
summarizes the results for different correlator types and samplings.
is the number of samples. Table6.1
summarizes the results for different correlator types and samplings.
Due to the discretization of the input voltages (as shown in
Fig.6.5), any knowledge of the absolute signal
value is lost. The signal amplitude is recovered by a regularly
performed calibration (using a calibration load of known
temperature, for details, see Chapter 12 by
A.Dutrey). Fig.6.6 shows the signal processing
steps from the incoming time series to the derived spectrum.
Figure 6.4:
Left:
Clipping correction (cross correlation coefficient of a continuous signal vs. cross
correlation correlation coefficient of a quantized signal) for two-, three- and four
level quantization (with optimized threshold voltage). The case of two level
quantization is also known as van Vleck correction. For more quantization
levels, the clipping correction becomes smaller. Right: Correlator efficiency as
function of the clipping voltage, for three-level and four-level quantization (at
Nyquist sampling).
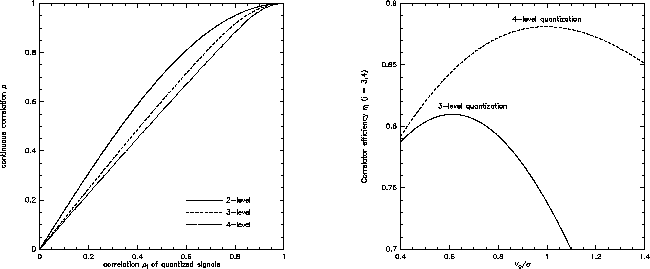 |
Figure 6.5:
Left:
Transfer function for a 4-level 2-bit correlator. The dashed line corresponds to the
transfer function of a (fictive) continuous correlator with an infinite number of
infinitesimally small delay steps. Right: Multiplication table. 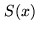 is the signal
bit at time
is the signal
bit at time 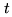 ,
, 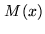 is the magnitude bit at time
is the magnitude bit at time 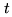 (respectively
(respectively 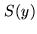 and
and
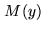 at time
at time 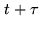 ).
).
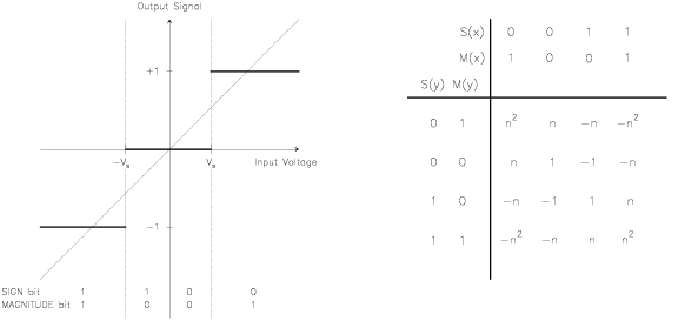 |
Figure 6.6:
The signal
processing in a 3-level 2-bit correlator. From top to bottom: the original
time series (sampled in discrete time steps, but continuous in amplitude), the
digitized time series (with high-level weight 3), the digital correlation
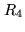 , the reconstructed spectral line.
, the reconstructed spectral line.
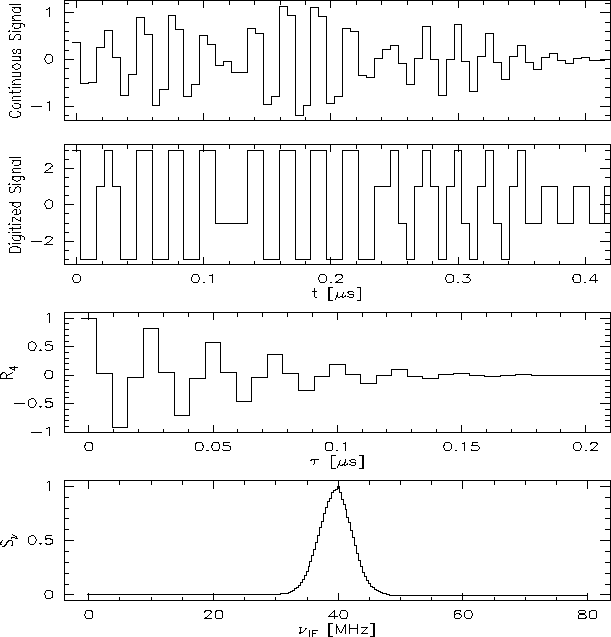 |
Table 6.1:
Correlator parameters for several quantization schemes
| method |
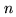 |
 [ [
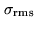 ] ] |
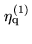 for for |
| |
|
|
sampling rate |
| |
|
|
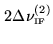 |
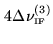 |
| two-level |
- |
- |
0.64 |
0.74 |
| three-level |
- |
0.61 |
0.81 |
0.89 |
| four-level |
3 |
1.00 |
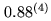 |
0.94 |
| |
4 |
0.95 |
0.88 |
0.94 |
 -level -level |
- |
- |
1.00 |
1.00 |
Notes:
(1) The correlator efficiency is defined by Eq.
6.13.
The values are for an idealized (rectangular)
bandpass and after level optimization.
(2) Nyquist sampling,
(3) oversampling by factor 2
(4) 0.87 if low level products deleted
(case of Plateau de Bure correlator)
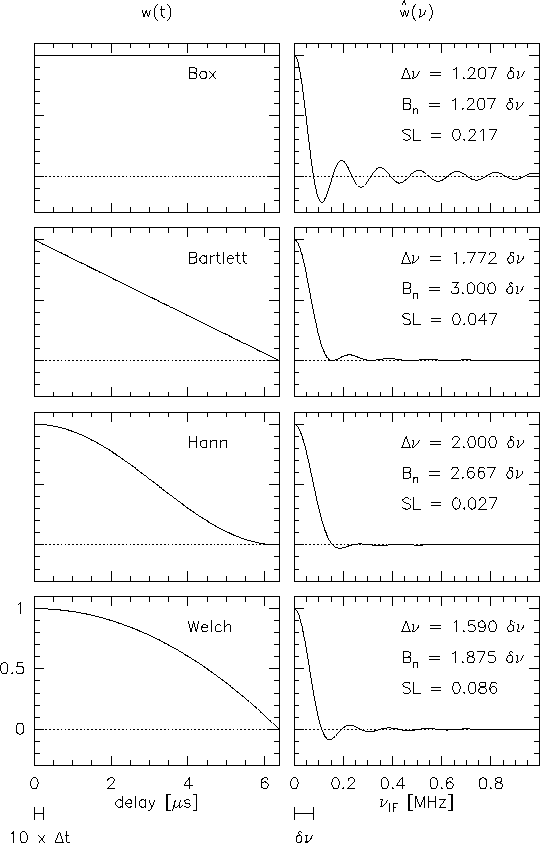
6.3.2 Time lag windows and spectral resolution
According to the sampling theorem, we need a
sampling timestep
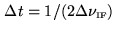 if we want to
fully recover the cross-power spectral density within a bandwidth
if we want to
fully recover the cross-power spectral density within a bandwidth
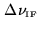 . The channel spacing
. The channel spacing 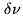 is then
determined by the maximum time lag
is then
determined by the maximum time lag
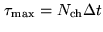 (where
(where
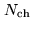 is the number of channels), i.e.
is the number of channels), i.e.
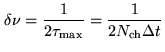 |
(6.13) |
However, the data acquisition is abruptly stopped after the maximum time
lag. After the Fourier transform, the observed cross power spectrum is thus
convolved with the Fourier transform
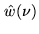 of the box-shaped time
window
of the box-shaped time
window 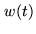 , producing strong sidelobes:
, producing strong sidelobes:
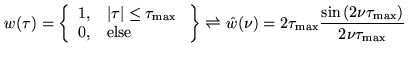 |
|
|
(6.14) |
These oscillations are especially annoying, if strong lines are observed. They
may be minimized, if the box-shaped time lag window is replaced by a function
that rises from zero to peak at negative time lags, and decreases to zero at
positive time lags (apodization). Such a window function suppresses the
sidelobes, at the cost of spectral resolution. A comparison between several
window functions is given in Fig.6.7, together with sidelobe
levels and spectral resolutions (defined by the full width at half-power,
FWHP, of the main lobe of the spectral window). Table 6.2
summarizes the various functions in time and spectral domains. The default of
the Plateau de Bure correlator is the Welch window, because it still offers a
good spectral resolution. Moreover, the oscillating sidelobes partly cancel out
the contamination of a channel by the signals in adjacent channels. Of course,
the observer is free to deconvolve the spectra from this default window, and to
use another time lag window.
Note: If you apodize your data, not only the effective spectral
resolution is changed. Due to the suppression of noise at large time lags,
the sensitivity is increased. The variance ratio of apodized data to
unapodized data,
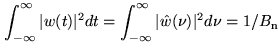 |
(6.15) |
defines the noise equivalent bandwidth 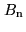 . It is the width of an
ideal rectangular spectral window (i.e.
. It is the width of an
ideal rectangular spectral window (i.e.
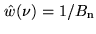 with zero
loss inside
with zero
loss inside
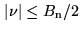 , and infinite loss outside) containing
the same noise power as the actual data. For sensitivity estimates of spectral
line observations, the channel width to be used is thus the noise equivalent
width, and neither the channel spacing, nor the effective spectral resolution.
Fig.6.7 gives the noise equivalent bandwidths
, and infinite loss outside) containing
the same noise power as the actual data. For sensitivity estimates of spectral
line observations, the channel width to be used is thus the noise equivalent
width, and neither the channel spacing, nor the effective spectral resolution.
Fig.6.7 gives the noise equivalent bandwidths 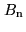 for
commonly used time lag windows.
for
commonly used time lag windows.
Figure:
Several time lag
windows, and their Fourier transforms (normalized to peak). The sidelobe levels SL
are indicated, as well as the spectral resolution (defined as the FWHP of the main
lobe), and the noise equivalent width. The delay stepsize, and channel spacing are
indicated for the following example: 256 channels, clock rate 40MHz, resulting in
a channel spacing of 78.125kHz.
 |
6.3.3 Main limitations
In real life, cross-correlators are subject to the performance of the
whole receiving system. This comprises the ``analog part'' (the signal
path from the receivers to the IF filters at the correlator entry),
and the ``digital part'' (everything behind the sampler).
Although the analog part is out of the correlator, its performance
requires to change our assumptions concerning the input data.
This complicates the analysis of the correlator response.
The following discussion refers to instantaneous errors only.
However, in interferometric mapping, scan-averaged visibilities are used,
and the data may be less affected.
The shape of the bandpass function (amplitude and phase) at the
correlator output is mainly due to the correlator's response to
the filters inserted in the IF band at the correlator entry. So
far, for the sake of simplicity, rectangular passbands, centered
at the intermediate frequency
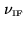 , have been assumed. A
more complex (and more realistic) case may be an amplitude slope
where the logarithm of the amplitude varies linearly with
frequency. Although the bandpass function will be calibrated (see
Eq.6.17, and R.Lucas Chapter 7), the
effect of such a slope on sensitivity remains. A derivation of the
signal-to-noise ratio for that case is beyond the scope of this
lecture. To give an impression of the order of magnitude: a slope
of 3.5dB (edge-to-edge) leads to a 2.5% degradation of the
sensitivity calculated for a rectangular passband. A center
frequency displacement of 5% of the bandwidth leads to the same
degradation.
, have been assumed. A
more complex (and more realistic) case may be an amplitude slope
where the logarithm of the amplitude varies linearly with
frequency. Although the bandpass function will be calibrated (see
Eq.6.17, and R.Lucas Chapter 7), the
effect of such a slope on sensitivity remains. A derivation of the
signal-to-noise ratio for that case is beyond the scope of this
lecture. To give an impression of the order of magnitude: a slope
of 3.5dB (edge-to-edge) leads to a 2.5% degradation of the
sensitivity calculated for a rectangular passband. A center
frequency displacement of 5% of the bandwidth leads to the same
degradation.
As already demonstrated, delay-setting errors linearly increase with the
intermediate frequency (Eq.6.6). Table6.3 gives an
impression of the decrease of sensitivity due to a delay error. The effect is
also shown in Fig.6.3 for a range of delay errors. For example, a
delay error of
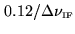 accounts for a 2.5% degradation. Delay
errors are mainly due to inaccurately known antenna positions (asking for a
better baseline calibration), or due to errors in the transmission cables.
accounts for a 2.5% degradation. Delay
errors are mainly due to inaccurately known antenna positions (asking for a
better baseline calibration), or due to errors in the transmission cables.
Table 6.3:
Effects of delay pattern on the sensitivity
| Intermediate frequency bandwidth |
 MHz MHz |
| Baseline |
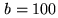 m m |
Zenith distance of source in direction
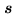 |
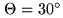 |
| Results in geometric delay: |
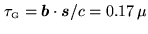 s s |
| Attenuation according to Eq.6.4 |
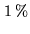 |
Phase errors across the bandpass may also be
of random nature. A phase fluctuation of
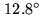 (rms) per scan leads to
a degradation of
(rms) per scan leads to
a degradation of
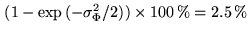 .
.
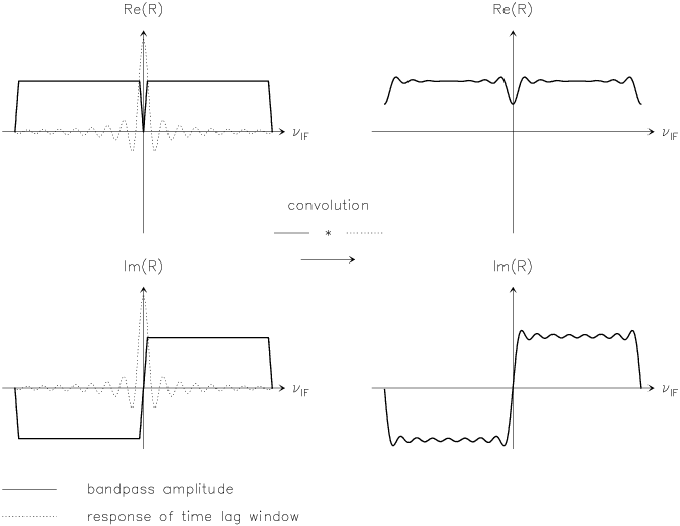
Figure 6.8:
The Gibbs phenomenon. The convolution of the bandpass
with the (unapodized) spectral window (sinc function) is shown for
the real and imaginary parts. Note that for the real part, the
phenomenon is stronger at the band edges, whereas for the
imaginary part, it contaminates the whole bandpass.
 |
Fluctuations across the bandpass also appear as ripples. They may
have several reasons, and are mainly due to the Gibbs
phenomenon, and due to reflections in the transmission cables. A
sinusoidal bandpass ripple of 2.9dB (peak-to-peak) yields a
2.5% degradation in the signal-to-noise ratio. The Gibbs
phenomenon also occurs in single-dish autocorrelation
spectrometers. For the sake of illustration, let us again assume a
perfectly flat response of receivers and filters. However, the
filter response function is only flat across the IF passband.
Towards its boundary, steep edges occur. We already learned that
strong spectral lines may show ripples, if no special data
windowing in time domain is applied. The Gibbs phenomenon is due
to a similar problem (but now the spectral line is replaced by the
edge of a flat rectangular band extending in frequency from zero
to
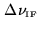 ). The output of the cosine correlator is
symmetric, but the sine output (imaginary part) is antisymmetric,
thus including an even steeper edge. Convolving this edge with the
sinc function (i.e. the spectral window) results in
strong oscillations. Let us call this function
). The output of the cosine correlator is
symmetric, but the sine output (imaginary part) is antisymmetric,
thus including an even steeper edge. Convolving this edge with the
sinc function (i.e. the spectral window) results in
strong oscillations. Let us call this function 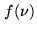 . For
calibration purposes, the Gibbs phenomenon has to be avoided: the
problem is that calibration uses the system response to a
flat-spectrum continuum source. A source whose visibility is
. For
calibration purposes, the Gibbs phenomenon has to be avoided: the
problem is that calibration uses the system response to a
flat-spectrum continuum source. A source whose visibility is
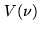 is seen as
is seen as
![$ f(\nu) \ast [G_{\rm ij}(\nu)V(\nu)]$](img749.png) (where
(where
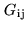 is now a frequency-dependent complex gain function).
After calibration it becomes
is now a frequency-dependent complex gain function).
After calibration it becomes
![$\displaystyle \hat{V}(\nu) = \frac{f(\nu)\ast [G_{\rm ij}(\nu)V(\nu)]}{f(\nu) \ast G_{\rm ij}(\nu)}$](img751.png) |
(6.16) |
Due to the convolution product the complex gain
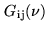 does not cancel out, as desired, and
does not cancel out, as desired, and
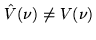 .
Automatic calibration procedures have to flag the channels
concerned. As shown in Fig.6.8, for the real part,
the effect is stronger at the band edges, but the output of the
imaginary part also shows ripples in the middle of the band (thus,
the problem is of greater importance for interferometers than for
single-dish telescopes using auto-correlators). If the bandwidth
to be observed is synthesized by two adjacent frequency windows,
the phenomenon is stronger at the band center. You should avoid to
place your line there, if it is on top of an important continuum
(see Section 6.4.1 for the case of the Plateau de Bure
system).
.
Automatic calibration procedures have to flag the channels
concerned. As shown in Fig.6.8, for the real part,
the effect is stronger at the band edges, but the output of the
imaginary part also shows ripples in the middle of the band (thus,
the problem is of greater importance for interferometers than for
single-dish telescopes using auto-correlators). If the bandwidth
to be observed is synthesized by two adjacent frequency windows,
the phenomenon is stronger at the band center. You should avoid to
place your line there, if it is on top of an important continuum
(see Section 6.4.1 for the case of the Plateau de Bure
system).
The above summary of the system-dependent performance of a correlator is not
exhaustive. For example, the phase stability of tunable filters, which depends
on their physical temperature, is not discussed. Alternatives to such filters
are image rejection mixers (as used in the Plateau de Bure correlator).
Errors induced by the digital part are generally negligible with respect to the
analog part. In digital delays, a basic limitation is given by the discrete
nature of the delay compensation, which accuracy in turn is limited by the
clock period of the sampler. However, digital techniques allow for high clock
rates, keeping this error at a minimum.
Evidently, a basic limitation is given by the memory of the counters,
setting the maximum time lag (which in turn defines the spectral resolution,
as already discussed): with 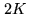 bits, we can exactly represent
bits, we can exactly represent 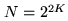 numbers. However, the information contained in the bits is not equivalent. For
the 3-level 2-bit correlator, the output of each channel
numbers. However, the information contained in the bits is not equivalent. For
the 3-level 2-bit correlator, the output of each channel 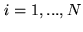 is
is
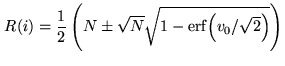 |
(6.17) |
(assuming white, Gaussian noise of zero mean and of unit variance, and
neglecting the weak contribution of the astrophysical signal). The
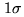 -precision of the output is
-precision of the output is
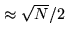 , contained in the
last
, contained in the
last 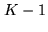 bits, which thus do not need to be transmitted. The maximum
integration time before overflow occurs is set by the number of bits of the
counter, and the clock frequency. Table6.4 shows
an example.
bits, which thus do not need to be transmitted. The maximum
integration time before overflow occurs is set by the number of bits of the
counter, and the clock frequency. Table6.4 shows
an example.
Table 6.4:
Maximum integration time of a 16-bit counter
| clock frequency: |
80MHz |
| weight for intermediate-level products: |
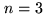 |
| positive offset: |
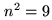 |
| weight for autocorrelation product: |
18 (using offset multiplication table) |
| carry out rate of a 4-bit adder |
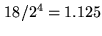 |
| maximum integration time: |
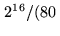 MHz MHz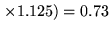 ms ms |
| same with a 4-bit prescaler: |
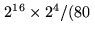 MHz MHz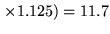 ms ms |
The only error cause due to the correlator that is worth to be
mentioned is the sampler, i.e. the analog-to-digital conversion.
As already shown, the threshold levels are adjusted with respect
to the noise in the unquantized signal. However, the noise power
may change during the integration. In that case, the correlator
does not operate anymore at its optimum level (see
Fig.6.4). This error cause can be eliminated with an
automatic level control circuit. However, slight deviations from
the optimal level adjustment may remain. Without going too far
into detail, the deviations can be decomposed in an even and an
odd part: in one case, the positive and negative threshold
voltages move into opposed directions (even part of the threshold
error). The resulting error can be equivalently interpreted as a
change of the signal level with respect to the threshold 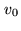 ,
and leads to a gain error. In the other case, the positive and
negative threshold voltages move into the same direction (odd part
of the threshold error). This error, however, can be reduced by
periodic sign reversal of the digitized samples (if the local
oscillator phase is simultaneously shifted by
,
and leads to a gain error. In the other case, the positive and
negative threshold voltages move into the same direction (odd part
of the threshold error). This error, however, can be reduced by
periodic sign reversal of the digitized samples (if the local
oscillator phase is simultaneously shifted by 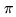 , the
correlator output remains unaffected). Combining the original and
phase-shifted outputs, the error cancels out with high precision.
Such a phase shift is implemented in the first local oscillators
of the Plateau de Bure system (for details see
Chapter 7 by R.Lucas). Note also that threshold
errors of up to 10% can be tolerated without degrading the
correlator sensitivity too much: the examination of
Fig.6.4 shows that such an error results in a
signal-to-noise degradation of less than 0.2% for a 3-level
system, and of less than 0.5% for a 4-level system (the maxima
of the efficiency curves are rather broad).
, the
correlator output remains unaffected). Combining the original and
phase-shifted outputs, the error cancels out with high precision.
Such a phase shift is implemented in the first local oscillators
of the Plateau de Bure system (for details see
Chapter 7 by R.Lucas). Note also that threshold
errors of up to 10% can be tolerated without degrading the
correlator sensitivity too much: the examination of
Fig.6.4 shows that such an error results in a
signal-to-noise degradation of less than 0.2% for a 3-level
system, and of less than 0.5% for a 4-level system (the maxima
of the efficiency curves are rather broad).
Another problem is that the nominal and actual threshold values may differ.
The error can be described by ``indecision regions''. By calculating the
probability that one or both signals of the cross-correlation product
fall into such an indecision region, the error can be estimated. With
an indecision region of 10% of the nominal threshold value, the
error is negligibly small.
Finally, it should be noted that strict synchronisation of the time series from
different antennas is mandatory: any deviation will introduce a phase error.




Next: 6.4 The correlator on
Up: 6. Cross Correlators
Previous: 6.2 Basic Theory
Contents
Anne Dutrey
![]() . The correlator
now proceeds in the following way: for each delay step
. The correlator
now proceeds in the following way: for each delay step ![]() ,
the corresponding sign and magnitude bits are put into two
registers (one for the first antenna, and one for the second). The
second register is successively shifted by one sample. In this
way, sample pairs from both antennas, separated by a successively
longer time lag, are created. These pairs are multiplied, using a
multiplication table. For the case of four-level quantization, it
is shown in Fig.6.5. Products which are assigned
a value of
,
the corresponding sign and magnitude bits are put into two
registers (one for the first antenna, and one for the second). The
second register is successively shifted by one sample. In this
way, sample pairs from both antennas, separated by a successively
longer time lag, are created. These pairs are multiplied, using a
multiplication table. For the case of four-level quantization, it
is shown in Fig.6.5. Products which are assigned
a value of ![]() are called ``high-level products'', those
with a value of
are called ``high-level products'', those
with a value of ![]() are ``intermediate-level products'', and
those with a value of
are ``intermediate-level products'', and
those with a value of ![]() ``low-level products''. The
products (evaluated using the multiplication table in
Fig.6.5) are sent to a counter (one counter for
each channel, i.e. for each of the discrete time lags). After the
end of the integration cycle, the counters are read out.
``low-level products''. The
products (evaluated using the multiplication table in
Fig.6.5) are sent to a counter (one counter for
each channel, i.e. for each of the discrete time lags). After the
end of the integration cycle, the counters are read out.
![]() , to avoid negative products (the offset
needs to be corrected when the counters are read out). This is
because the counter is simply an adding device. As another
simplification, low-level products may be deleted. This makes
digital implementation easier, and accounts for a loss of
sensitivity of merely 1% (see Table 6.1). Finally,
not all bits of the counters' content need to be transmitted (see
Section 6.3.2).
, to avoid negative products (the offset
needs to be corrected when the counters are read out). This is
because the counter is simply an adding device. As another
simplification, low-level products may be deleted. This makes
digital implementation easier, and accounts for a loss of
sensitivity of merely 1% (see Table 6.1). Finally,
not all bits of the counters' content need to be transmitted (see
Section 6.3.2).
![$\displaystyle N_{01,01} = NP_{01,01} = \frac{N}{2\pi\sigma^2\sqrt{1-\rho^2}} \i...
...nfty}{ \exp{\left[\frac{-(x^2+y^2-2\rho xy)}{2\sigma^2(1-\rho^2)}\right]}dx}dy}$](img698.png)
![]() means
k-level quantization). The integrand may be replaced by an interpolating
polynomial, allowing to solve the integral. One may also construct
an interpolating surface
means
k-level quantization). The integrand may be replaced by an interpolating
polynomial, allowing to solve the integral. One may also construct
an interpolating surface
![]() . As already discussed, the
clipping correction cannot recover the loss of sensitivity due to
quantization. The loss of sensitivity for
. As already discussed, the
clipping correction cannot recover the loss of sensitivity due to
quantization. The loss of sensitivity for ![]() -level discretization may be
found by evaluating the signal-to-noise ratio
-level discretization may be
found by evaluating the signal-to-noise ratio
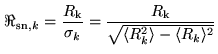



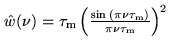
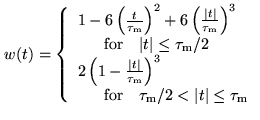
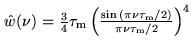
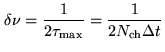
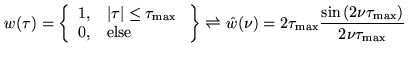
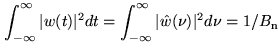

![]() accounts for a 2.5% degradation. Delay
errors are mainly due to inaccurately known antenna positions (asking for a
better baseline calibration), or due to errors in the transmission cables.
accounts for a 2.5% degradation. Delay
errors are mainly due to inaccurately known antenna positions (asking for a
better baseline calibration), or due to errors in the transmission cables.
![]() (rms) per scan leads to
a degradation of
(rms) per scan leads to
a degradation of
![]() .
.

![]() bits, we can exactly represent
bits, we can exactly represent ![]() numbers. However, the information contained in the bits is not equivalent. For
the 3-level 2-bit correlator, the output of each channel
numbers. However, the information contained in the bits is not equivalent. For
the 3-level 2-bit correlator, the output of each channel ![]() is
is
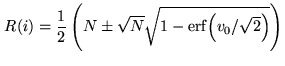
![]() ,
and leads to a gain error. In the other case, the positive and
negative threshold voltages move into the same direction (odd part
of the threshold error). This error, however, can be reduced by
periodic sign reversal of the digitized samples (if the local
oscillator phase is simultaneously shifted by
,
and leads to a gain error. In the other case, the positive and
negative threshold voltages move into the same direction (odd part
of the threshold error). This error, however, can be reduced by
periodic sign reversal of the digitized samples (if the local
oscillator phase is simultaneously shifted by ![]() , the
correlator output remains unaffected). Combining the original and
phase-shifted outputs, the error cancels out with high precision.
Such a phase shift is implemented in the first local oscillators
of the Plateau de Bure system (for details see
Chapter 7 by R.Lucas). Note also that threshold
errors of up to 10% can be tolerated without degrading the
correlator sensitivity too much: the examination of
Fig.6.4 shows that such an error results in a
signal-to-noise degradation of less than 0.2% for a 3-level
system, and of less than 0.5% for a 4-level system (the maxima
of the efficiency curves are rather broad).
, the
correlator output remains unaffected). Combining the original and
phase-shifted outputs, the error cancels out with high precision.
Such a phase shift is implemented in the first local oscillators
of the Plateau de Bure system (for details see
Chapter 7 by R.Lucas). Note also that threshold
errors of up to 10% can be tolerated without degrading the
correlator sensitivity too much: the examination of
Fig.6.4 shows that such an error results in a
signal-to-noise degradation of less than 0.2% for a 3-level
system, and of less than 0.5% for a 4-level system (the maxima
of the efficiency curves are rather broad).