7.4 The PdB Signal and LO transport system

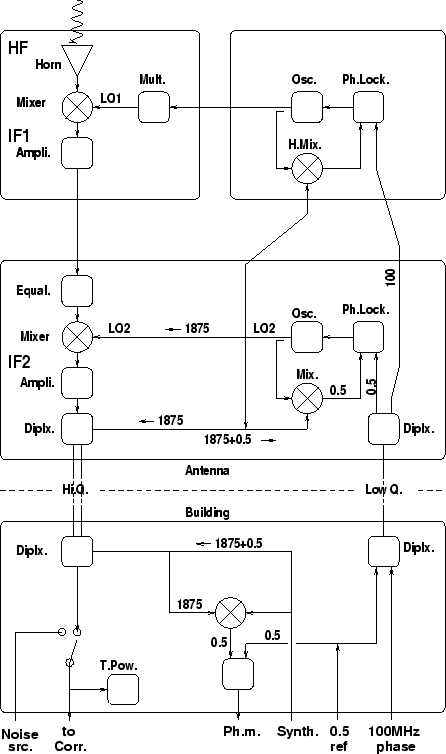
A block diagram of the Plateau de Bure interferometer system is shown in Fig. 7.3.

Figure 7.3: The Plateau de Bure interferometer system

7.4.1 Signal path

The signal path is outlined in Fig. 7.3. It shows the signal and LO paths for one antenna and one receiver band. The high frequency part (receiver) was described in Chapter 5. The amplified first IF output (1275-1775 MHz) is down-converted to the $100-600$ MHz band and transported to the central building in a high-quality cable. Before down-conversion, the band shape is modified by a low-pass filter; since the LO2 is at a higher frequency than the IF2, the bandpass will be reversed in the conversion, and this by anticipation compensates for the frequency dependent attenuation in the cable (which is of course higher at the high-frequency end of the bandpass).

The $100-600$ MHz band arriving in the central building is directed to the correlator analog IF processor inputs (with a division by 6 since there are 6 identical correlator units) and to total power detectors which are used for the atmospheric calibration and for the radiometric phase correction.

7.4.2 LO generation

The first local oscillator is a Gunn oscillator (a tripler is used for the 1.3mm receiver). The Gunn is phase-locked by mixing part of its output with a harmonic of a reference signal (used also as the second LO): the harmonic mixing produces a 100MHz signal, the phase of which is compared to a reference signal at frequency $\epsilon_\mathrm{\scriptscriptstyle 1}$$= 100$MHz, coming from the central building. That reference signal is used to carry the phase commands to be applied to the first LO: a continuously varying phase to compensate for earth motion and phase switching used to separate the side-bands and suppress offsets.

The LO1 signal at $\nu_\mathrm{\scriptscriptstyle LO1}$ may be locked either 100MHz above (``High Lock'') or below (``Low Lock'') the $\ensuremath{N_\mathrm{\scriptscriptstyle H}}^{\rm th}$ harmonic of the LO2 frequency $\nu_\mathrm{\scriptscriptstyle LO2}$:

$$\ensuremath{\nu_\mathrm{\scriptscriptstyle LO1}}= (\ensuremath{N_... ...on_\mathrm{\scriptscriptstyle 1}}) \ensuremath{N_\mathrm{\scriptscriptstyle M}}$$ (7.17)

The multiplication factor $N_\mathrm{\scriptscriptstyle M}$ is 1 for the 3mm receiver and 3 for the 1.3mm receiver.

The second local oscillator, at $\ensuremath{\nu_\mathrm{\scriptscriptstyle LO2}}=1875\pm25$ MHz, is phase locked $\epsilon_\mathrm{\scriptscriptstyle 2}$=0.5 MHz below the frequency sent by the synthesizer in the central building (which is under computer control and common to all antennas):

$$\ensuremath{\nu_\mathrm{\scriptscriptstyle LO2}}= \ensuremath{\nu... ...m{\scriptscriptstyle SYN}}- \ensuremath{\epsilon_\mathrm{\scriptscriptstyle 2}}$$ (7.18)

The $\epsilon_\mathrm{\scriptscriptstyle 2}$ reference frequency is sent to all antennas from the central building in a low quality cable, together with the $\epsilon_\mathrm{\scriptscriptstyle 1}$$= 100$MHz reference frequency for the first LO. The $\nu_\mathrm{\scriptscriptstyle SYN}$ is sent to the antennas via the same high-Q cable that transports the IF2 signal. No phase rotation is applied on the second local oscillator. The relation between the RF signal frequencies (in the local rest frame) in the upper and lower sidebands and the signal frequency in the second IF band is thus (for high lock):

$$\ensuremath{\nu_\mathrm{\scriptscriptstyle U}}= \ensuremath{\nu_\... ...mathrm{\scriptscriptstyle 1}}- \ensuremath{\nu_\mathrm{\scriptscriptstyle IF2}}$$ (7.19)

and in the lower sideband:

$$\ensuremath{\nu_\mathrm{\scriptscriptstyle L}}= \ensuremath{\nu_\... ...mathrm{\scriptscriptstyle 1}}+ \ensuremath{\nu_\mathrm{\scriptscriptstyle IF2}}$$ (7.20)

7.4.3 Further signal processing

In each correlator a variable section of the IF2 band is down-converted to baseband by means of two frequency changes, with a fixed third LO (LO3) and a tunable fourth LO (LO4). It is on that LO4 that the phase rotations needed to compensate for residual phase drifts due to the geometrical delay change are applied (in fact that LO4 plays the role of the second frequency conversion in the above analysis). No phase rotation is applied on the second and third local oscillators.

The phase rotation applied on the fourth LO's is:

$$\ensuremath{\varphi_\mathrm{\scriptscriptstyle LO4}}= (\ensuremat... ...athrm{\scriptscriptstyle LO4}}) \ensuremath{\tau_\mathrm{\scriptscriptstyle G}}$$ (7.21)

since the second and third conversions are LSB while the fourth is USB. It is different in the different correlator units since the $\omega_\mathrm{\scriptscriptstyle LO4}$ frequencies are different.

7.4.4 Phase stability requirements

Short term phase errors in the local oscillators (jitter) will cause a decorrelation of the signal and reduce the visibility amplitude by a factor

$$\ensuremath{\eta_\mathrm{\scriptscriptstyle 12}}= e^{-({\sigma_1}... ..._\mathrm{\scriptscriptstyle 1}}\ensuremath{\eta_\mathrm{\scriptscriptstyle 2}}}$$ (7.22)

where $\sigma_1$ is the rms phase fluctuation of the LO in one of the antennas ($\sigma_2$ in the other). $\ensuremath{\eta_\mathrm{\scriptscriptstyle 1}} = e^{-{\sigma_1}^2 }$ is the decorrelation factor for one antenna; typical requirements on $\sigma_1$ are:

$\ensuremath{\eta_\mathrm{\scriptscriptstyle 1}}$	0.99	0.98	0.95	0.90
$\sigma_1$ (degrees)	5.75	8.1	13.0	18.5

The phase stability required on the LO2 is $\sigma_1/(\ensuremath{N_\mathrm{\scriptscriptstyle M}}\ensuremath{N_\mathrm{\scriptscriptstyle H}}) \sim 0.1^\circ$ for a 0.95 efficiency at 1.3mm: very stable oscillators are needed.

7.4.5 Cable electrical length control

The $\epsilon_\mathrm{\scriptscriptstyle 2}$ reference frequency is also used for a continuous control of the electrical length of the High-Q cables transporting the IF2 signal from the antennas to the correlator room in the central building. A variation $\Delta L$ in the electrical length of the High-Q cable will affect the signal phase by $360 \Delta L/\ensuremath{\lambda_\mathrm{\scriptscriptstyle IF2}}$; for a length of 500m and a temperature coefficient of $10^{-5}$ we have a variation in length of 5mm or 17ps, which translates into a phase shift of 4 degrees at the high end of the passband: this is a very small effect.

The same length variation induces a phase shift of $360 \times 0.017 \times 1.875 = 11.5$ degrees at the LO2 frequency. This signal being multiplied by $(\ensuremath{N_\mathrm{\scriptscriptstyle H}}+1)\ensuremath{N_\mathrm{\scripts... ...criptscriptstyle U}}/ \ensuremath{\nu_\mathrm{\scriptscriptstyle LO2}} \sim 120$ for the 1.3mm receiver, we have a totally unacceptable shift of about 4 turns. The cables are buried in the ground for most of their length; however they also run up the antennas and suffer from varying torsions when the sources are tracked, and in particular when the antenna is moved from the source to a phase calibrator.

For this reason the electrical length of the cables is under permanent control. The LO2 signal is sent back to the central building in the High Q cable, and there it is mixed with the $\ensuremath{\nu_\mathrm{\scriptscriptstyle LO2}}+\ensuremath{\epsilon_\mathrm{\scriptscriptstyle 2}}$ signal from the synthesizer. The phasemeter measures every second the phase difference between the beat signal at 0.5 MHz and a reference 0.5 MHz signal.

The measured phase difference is twice the phase offset affecting the LO2, it is used by the computer to correct the LO1 phase $\varphi_\mathrm{\scriptscriptstyle LO1}$ after multiplication by $\ensuremath{\nu_\mathrm{\scriptscriptstyle LO1}} / \ensuremath{\nu_\mathrm{\scriptscriptstyle LO2}}$.