Sampling on a regular grid is equivalent to multiplying by a series of periodically
spaced delta functions, i.e. the so-called shah function
![]() :
:
![$\displaystyle [\frac{1}{\Delta u}] \ensuremath{\mathrm{III}}(\frac{u}{\Delta u}) = \sum_{k=-\infty}^{\infty} \delta(u-k\Delta u)$](img1565.png) |
(15.10) |
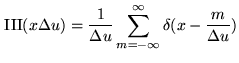 |
(15.11) |
Hence, sampling the visibilities ![]() results in convolving its Fourier Transform
results in convolving its Fourier Transform
![]() by a periodic shah function. This convolution reproduces in a periodic
way the Fourier Transform of the visibilities
by a periodic shah function. This convolution reproduces in a periodic
way the Fourier Transform of the visibilities ![]() .
.
If the Fourier Transform of the visibilities ![]() , i.e. the brightness
distribution
, i.e. the brightness
distribution ![]() , has finite support
, has finite support ![]() , the replication poses no problem
provided the support is smaller than the periodicity of the shah function,
i.e.
, the replication poses no problem
provided the support is smaller than the periodicity of the shah function,
i.e.
| (15.12) |
In aperture synthesis, finite support is ensured to first order by the finite width
of the antenna primary beam ![]() . However, strong sources in the antenna sidelobes
may be aliased if the imaged area is too small. Moreover, the noise does not
have finite support. White noise in the
. However, strong sources in the antenna sidelobes
may be aliased if the imaged area is too small. Moreover, the noise does not
have finite support. White noise in the ![]() plane would result in white noise in
the map plane. In practice, the noise in the
plane would result in white noise in
the map plane. In practice, the noise in the ![]() plane is not completely white.
However, it is support limited (since only a finite region of the
plane is not completely white.
However, it is support limited (since only a finite region of the ![]() plane is
sampled in any experiment). Accordingly, its Fourier Transform in the map plane is
not support limited. Noise aliasing thus occurs, and produces an increased noise
level at the map edges.
plane is
sampled in any experiment). Accordingly, its Fourier Transform in the map plane is
not support limited. Noise aliasing thus occurs, and produces an increased noise
level at the map edges.