Next: 7. LO System and
Up: 6. Cross Correlators
Previous: 6.4 The correlator on
Contents
Subsections
- Cross-correlation function of voltage outputs
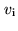 and
and 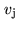 from antenna pair
from antenna pair 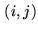 :
:
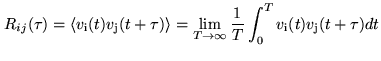 |
(6.18) |
- Covariance of two jointly random variables:
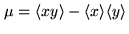 |
(6.19) |
For signals of zero mean, and again identifying
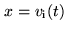 and
and
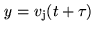 ,
,
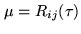 |
(6.20) |
- Cross-correlation coefficient of two jointly random variables
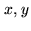 of variance
of variance
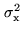 and
and
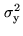 :
:
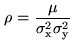 |
(6.21) |
For jointly normal random variables of zero mean and of variance
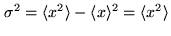 ,
and with
,
and with
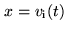 and
and
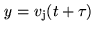 , the cross-correlation
function
, the cross-correlation
function
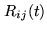 and the cross-correlation coefficient are related by
and the cross-correlation coefficient are related by
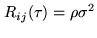 |
(6.22) |
- Bivariate Gaussian Probability Distribution:
Assume two Gaussian random variables 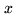 and
and 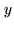 , both of
zero mean, and variance
, both of
zero mean, and variance 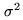 . The probability
. The probability
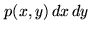 that the value of
that the value of 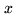 is between
is between 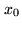 and
and 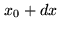 ,
and that simultaneously the value of
,
and that simultaneously the value of 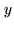 between
between 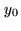 and
and 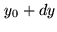 ,
is given by the jointly gaussian probability distribution
,
is given by the jointly gaussian probability distribution
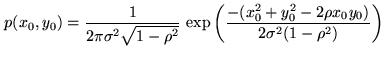 |
(6.23) |
In our case, the variable 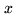 is assigned to the output voltage of antenna
is assigned to the output voltage of antenna
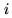 at time
at time 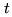 , and
, and 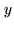 the output voltage of antenna
the output voltage of antenna 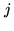 at time
at time 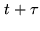 .
.
The following determination of the clipping correction is due to
[Hagen et al. 1973]:
Given two jointly normal random variables 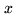 and
and 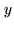 with covariance
with covariance 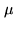 ,
and given some arbitrary function
,
and given some arbitrary function 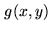 , Price's theorem states that
, Price's theorem states that
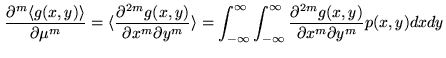 |
(6.24) |
For random signals of zero mean, the covariance 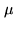 is identical with the
cross-correlation function
is identical with the
cross-correlation function
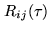 defined in Eq.6.1. As
shown by Eq.6.1, we need to accumulate products of the voltage
outputs of two antennas
defined in Eq.6.1. As
shown by Eq.6.1, we need to accumulate products of the voltage
outputs of two antennas 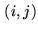 , but using the quantized signals rather than
the continuous ones. Thus, with
the identification
, but using the quantized signals rather than
the continuous ones. Thus, with
the identification
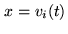 and
and
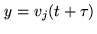 , and using
, and using 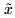 and
and 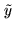 for the quantized signals, we can apply Price's theorem to the
4-level cross-correlation function
for the quantized signals, we can apply Price's theorem to the
4-level cross-correlation function
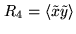 such that
such that
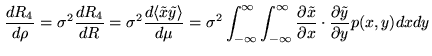 |
(6.25) |
(
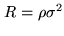 denotes the continuous cross correlation function,
for the sake of simplicity, antenna indices are omitted). The partial
derivatives in the integrand are easily found by using the transfer function
shown in Fig.6.5:
denotes the continuous cross correlation function,
for the sake of simplicity, antenna indices are omitted). The partial
derivatives in the integrand are easily found by using the transfer function
shown in Fig.6.5:
![$\displaystyle \tilde{x} = \Theta(x)+(n-1)\left[\Theta(x-v_0)-\Theta(-x-v_0) \right] \Theta(-x)$](img825.png) |
(6.26) |
where
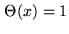 for
for 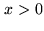 , and 0 else. Thus,
, and 0 else. Thus,
![$\displaystyle \frac{\partial \tilde{x}}{\partial x} = 2\delta(x)+(n-1)\left[ \delta(x-v_0)+\delta(x+v_0)\right]$](img828.png) |
(6.27) |
Re-writing Price's theorem, we find
Inserting the jointly normal distribution 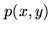 , and evaluating the
integral yields
, and evaluating the
integral yields
or, alternatively, the integral form given in Eq.6.11.




Next: 7. LO System and
Up: 6. Cross Correlators
Previous: 6.4 The correlator on
Contents
Anne Dutrey
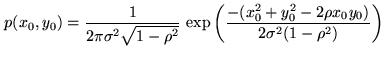
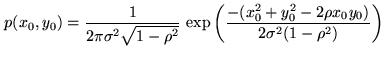
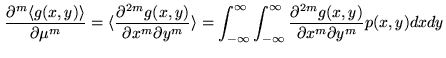
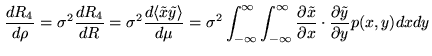
![$\displaystyle \frac{\partial \tilde{x}}{\partial x} = 2\delta(x)+(n-1)\left[ \delta(x-v_0)+\delta(x+v_0)\right]$](img828.png)
![$\displaystyle \sigma^2 \int_{-\infty}^{\infty}
{\int_{-\infty}^{\infty}{
\left(2\delta(x)+(n-1)\left[\delta(x-v_0)+\delta(x+v_0)\right]
\right)}}$](img830.png)
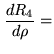
![$\displaystyle \frac{\sigma^2}{\pi}
\frac{1}{\sqrt{1-r^2}}\biggl\{(n-1)^2
\left[...
...a^2(1+\rho)}\right)}+
\exp{\left(\frac{-v_0^2}{\sigma^2(1-\rho)}\right)}\right]$](img834.png)