As has been seen in the previous lectures, each interferometer
baseline provides a measurement of the source visibility at a given
point in the ![]() plane of spatial frequencies; the source
brightness distribution can then be reconstructed by an appropriate
Fourier Transform.
plane of spatial frequencies; the source
brightness distribution can then be reconstructed by an appropriate
Fourier Transform.
In reality things are not so simple. Interferometers are designed with a lot of care; however many electronic components will have variable gains both in amplitude and in phase; these variations will affect the results and have to be taken out. It is generally sometimes more efficient to have a slightly varying instrument response, and a more sensitive instrument, than a very stable one with less sensitivity, provided the varying terms in the response are slow and may be easily calibrated out. At millimeter wavelengths the atmospheric absorption and path length fluctuations will dominate the instrument imperfections in most cases.
For a given observation, if we interpret the correlator response
(amplitude and phase) as the source visibility, ignoring any
imperfections, we have an observed (apparent) visibility
![]() , where
, where ![]() are antenna numbers,
are antenna numbers, ![]() the frequency
and
the frequency
and ![]() is time. If the true source visibility is
is time. If the true source visibility is
![]() , we
may define :
, we
may define :
Since amplitude and phase distortions have different physical origins it is generally useful to write
| (9.2) |
The baseline-based gains can be determined by observing a point
source. This is usually a strong quasar. In that case the true
visibilities
![]() should all be equal to the quasar flux
density
should all be equal to the quasar flux
density ![]() . Then
. Then
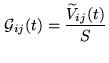 |
(9.3) |
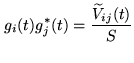 |
(9.4) |
If we note
![]() ,
the equations for phases are simply:
,
the equations for phases are simply:
| (9.5) |
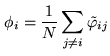 |
(9.6) |
| (9.7) | |||
| (9.8) |
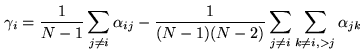 |
(9.9) |
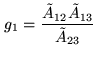 |
(9.10) |
It can be seen in the above formulas that the precision to which the
antenna phases and amplitudes is determined is improved by a factor ![]() over the precision of the measurement of the baseline amplitudes and
phases.
over the precision of the measurement of the baseline amplitudes and
phases.
The determination of antenna-based gains (amplitudes and phases) has an obvious advantage: the physical cause of the gain variations are truly antenna-based. One may solve for the gains at the time of the observations, and correct the occurring problems to improve the quality of the data. One may re-point or re-focus the antennas to correct for an amplitude loss, correct for an instrumental delay (affecting the frequency dependence of the phases) ...