



Next: 10.2.2 Absolute errors on Tcal
Up: 10.2 Single-dish Calibration of
Previous: 10.2 Single-dish Calibration of
When the opacity of the atmosphere is weak (
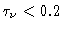 ) and equal in
both image and signal bands, Tcal is mostly dependent of Tatm and
both of them can be considered as independent of
) and equal in
both image and signal bands, Tcal is mostly dependent of Tatm and
both of them can be considered as independent of 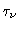 and hence w.
and hence w.
In the conditions mentioned above, 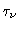 can be eliminated from Eq.10.5.
The equation becomes:
can be eliminated from Eq.10.5.
The equation becomes:
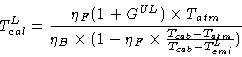 |
(10.11) |
(details about the derivation of Eq.10.11 are given in the documentation
``Amplitude Calibration'' by S.Guilloteau). In Eq.10.11, the unknown is
Tatm, the physical temperature of the absorbing layers. Tatm is mostly
dependent on the outside temperature, pressure and site altitude and weakly on
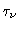 . For this reason, Tcal and Tsys remain correct even if w and
hence
. For this reason, Tcal and Tsys remain correct even if w and
hence 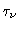 are not properly constrained.
are not properly constrained.
Figures 10.1 and 10.2 illustrate this point. Thick lines correspond to
the exact equation (Eq.10.5) and dashed lines to the approximation
(Eq.10.11). The comparison between Eq.10.11 and 10.5 was done for three
common cases 1) at 87 GHz, with
GUL=10-2, 2) at 115 GHz, with
GLU=0.5and at 230 GHz, with
GUL=0.5. For the 15-m dishes, the forward efficiencies
used are
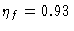 at 3mm and
at 3mm and
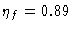 at 1.3mm. Fig.10.1 is
done for a source at
elevation=200 and Fig.10.2 for a source at
elevation=60o.
at 1.3mm. Fig.10.1 is
done for a source at
elevation=200 and Fig.10.2 for a source at
elevation=60o.
Figure 10.1:
Calibration temperature as
function of water vapor (or opacity) at 87, 115 and 230 GHz for a source at 20
degrees elevation. Parameters are taken for the Bure interferometer.
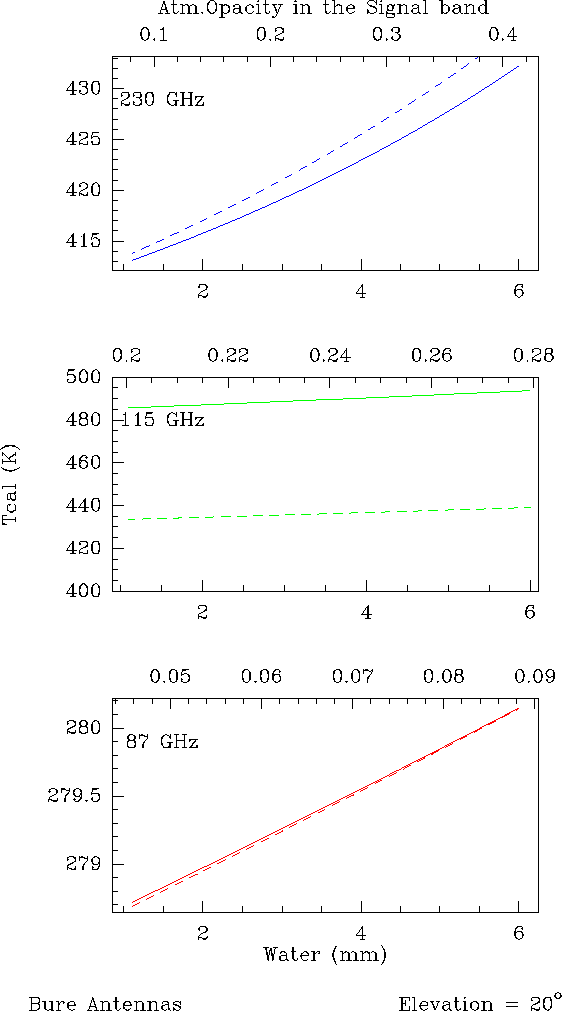 |
Figure 10.2:
Calibration temperature as
function of water vapor (or opacity) at 87, 115 and 230 GHz for a source at 60
degrees elevation. Parameters are taken for the Bure interferometer.
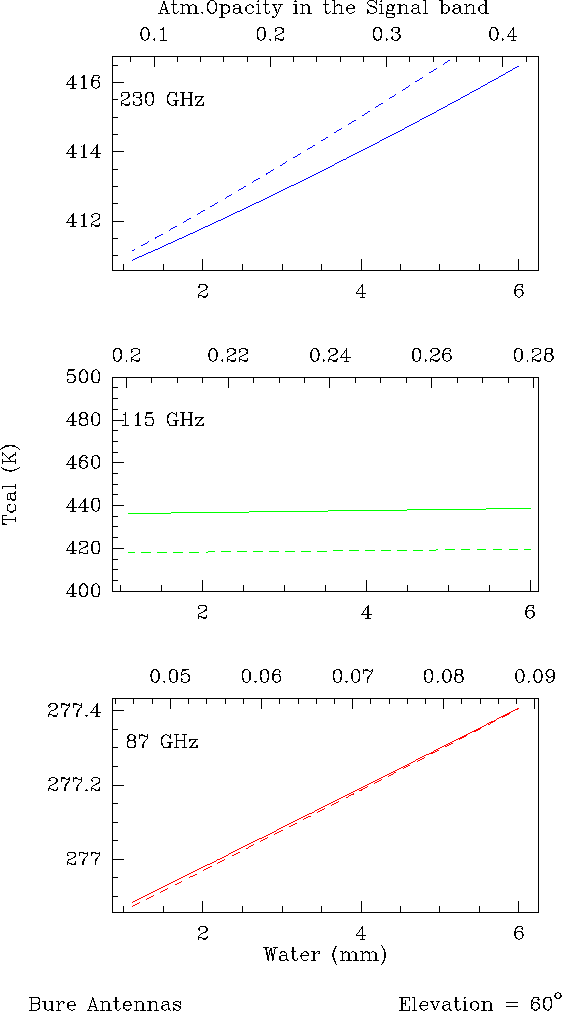 |
The following points can be deduced from these figures:
- 1.
- As long as
TskyL=TskyU, the equation 10.11 remains
valid even at high frequencies > 200 GHz and for w> 5 mm.
- 2.
- This comes from the fact the Tatm is mostly independent of
the atmospheric water vapor content.
- 3.
- As soon as
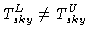 ,
the equation 10.11
is not valid. Note also that the error is about constant with the opacity because
Tatm is mostly independent of the atmospheric water vapor content. Moreover at
115 GHz, the atmospheric opacity is dominated by the 118 GHz Oxygen line and cannot
be below 0.2, the amount of opacity added by the water vapor is small. Tcalremains mostly constant with w.
,
the equation 10.11
is not valid. Note also that the error is about constant with the opacity because
Tatm is mostly independent of the atmospheric water vapor content. Moreover at
115 GHz, the atmospheric opacity is dominated by the 118 GHz Oxygen line and cannot
be below 0.2, the amount of opacity added by the water vapor is small. Tcalremains mostly constant with w.
At mm wavelengths, the derivation of the Tcal (or Tsys) using an
atmospheric model is then quite safe.




Next: 10.2.2 Absolute errors on Tcal
Up: 10.2 Single-dish Calibration of
Previous: 10.2 Single-dish Calibration of
S.Guilloteau
2000-01-19
![]() ) and equal in
both image and signal bands, Tcal is mostly dependent of Tatm and
both of them can be considered as independent of
) and equal in
both image and signal bands, Tcal is mostly dependent of Tatm and
both of them can be considered as independent of ![]() and hence w.
and hence w.
![]() can be eliminated from Eq.10.5.
The equation becomes:
can be eliminated from Eq.10.5.
The equation becomes:
![]() at 3mm and
at 3mm and
![]() at 1.3mm. Fig.10.1 is
done for a source at
elevation=200 and Fig.10.2 for a source at
elevation=60o.
at 1.3mm. Fig.10.1 is
done for a source at
elevation=200 and Fig.10.2 for a source at
elevation=60o.

