



Next: 10.2.1 Low opacity approximation Tcal
Up: 10. Amplitude and Flux
Previous: 10.1 Definition and Formalism
10.2 Single-dish Calibration of the Amplitude
This calibration is done automatically and in real-time but it can be redone
a posteriori if one or several parameters are wrong using the CLIC command
ATMOSPHERE. However, for 99 % of the projects, the single-dish calibration is
correct. Moreover, we will see in this section that in most cases, even with
erroneous calibration parameters, it is almost impossible to do an error larger than
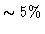 .
.
For details about the properties of the atmosphere, the reader has to refer to the
lecture by M.Bremer (Chapter 9) while the transmission of the atmosphere
at mm wavelengths is described in the lecture of M.Guélin (Chapter 8).
Most of this lecture is extracted from the documentation ``Amplitude Calibration''
by S.Guilloteau for single-dish telescope and from [Guilloteau et al 1993].
Since all this part of the calibration is purely antenna dependent and in order to
simplify the equations, the subscript i will be systematically ignored. In the
same spirit, the equations will be expressed in TA* scale taking
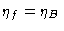 .
.
The atmospheric absorption (e.g. for the Lower side-band TcalL) can be
expressed by
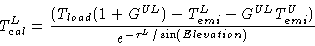 |
(10.5) |
where Tload is the hot load and TemiL and TemiU are the noise
temperature received from the sky in the lower an upper sidebands respectively (for
the IRAM interferometer, the difference in frequency between the upper and lower
sidebands is 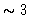 GHz).
GHz).
The system temperature Tsys is given by:
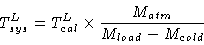 |
(10.6) |
The main goal of the single-dish calibration is to measure Tcal (hence
Tsys) as accurately as possible.
At Bure, during an atmospheric calibration, the measured quantities are:
- Phase 1, Matm: the power received from the sky
- Phase 2, Mload: the power received from the hot load
- (Phase 3), Mcold: the power received from the cold load
Trec, the noise temperature of the receiver, is deduced from the measurements
on the hot and cold loads at the beginning of each project and regularly checked.
The receiver sideband ratio GUL is also measured at the beginning of each
project (see R.Lucas lecture 7). Temi, the effective temperature
seen by the antenna, is given by
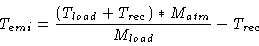 |
(10.7) |
Moreover, Temi which is measured on the bandwidth of the receiver, can be
expressed as the sum of TemiL and TemiU (a similar expression exists for
Tsky):
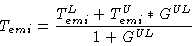 |
(10.8) |
Temi is directly linked to the sky temperature emissivity (or brightness
temperature) Tsky by:
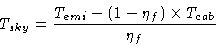 |
(10.9) |
were Tcab is the physical temperature inside the cabin and 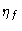 , the
forward efficiency, which are both known (or measurable) quantities.
, the
forward efficiency, which are both known (or measurable) quantities.
Our calibration system provides then a direct measurement of Temi and hence of
Tsky, which is deduced from quantities accurately measured. Hence, in
Eq.10.5 the only unknown parameter remains 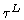 , the opacity of the
atmosphere at zenith, which is iteratively computed together with Tatm the
physical atmospheric temperature of the absorbing layers. This calculation is
performed by the atmospheric transmission model ATM (see Chapter 8) and
the documentation ``Amplitude Calibration'').
, the opacity of the
atmosphere at zenith, which is iteratively computed together with Tatm the
physical atmospheric temperature of the absorbing layers. This calculation is
performed by the atmospheric transmission model ATM (see Chapter 8) and
the documentation ``Amplitude Calibration'').
The opacity 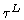 (or more generally
(or more generally 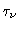 ) comes from two terms:
) comes from two terms:
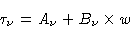 |
(10.10) |
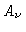 and
and 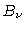 are the respective contributions to O2 and H2O, the water
vapor content w is then adjusted with Tatm by the model ATM to match the
measured Tsky. The ATM model works as long as the hypothesis done on the
structure of the atmosphere in plane-parallel layers is justified, as it is usually
the case for standard weather conditions.
are the respective contributions to O2 and H2O, the water
vapor content w is then adjusted with Tatm by the model ATM to match the
measured Tsky. The ATM model works as long as the hypothesis done on the
structure of the atmosphere in plane-parallel layers is justified, as it is usually
the case for standard weather conditions.




Next: 10.2.1 Low opacity approximation Tcal
Up: 10. Amplitude and Flux
Previous: 10.1 Definition and Formalism
S.Guilloteau
2000-01-19
![]() .
.
![]() .
.
![]() , the opacity of the
atmosphere at zenith, which is iteratively computed together with Tatm the
physical atmospheric temperature of the absorbing layers. This calculation is
performed by the atmospheric transmission model ATM (see Chapter 8) and
the documentation ``Amplitude Calibration'').
, the opacity of the
atmosphere at zenith, which is iteratively computed together with Tatm the
physical atmospheric temperature of the absorbing layers. This calculation is
performed by the atmospheric transmission model ATM (see Chapter 8) and
the documentation ``Amplitude Calibration'').
![]() (or more generally
(or more generally ![]() ) comes from two terms:
) comes from two terms: