


Next: 14.3 Experimental data space
Up: 14. Advanced Imaging Methods:
Previous: 14.1 Introduction
In the problems of Fourier synthesis encountered in astronomy,
the object function of interest,
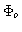 , is a
real-valued function of an angular position variable
, is a
real-valued function of an angular position variable
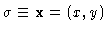 . The geometrical elements
under consideration are presented in Fig. 14.1.
. The geometrical elements
under consideration are presented in Fig. 14.1.
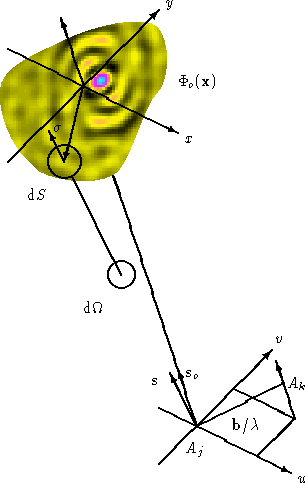
Figure:
Traditional coordinate systems used to express the
relation between the complex visibilities and the brightness distribution
of a source under observation. Here, the two antennas Aj and Akpoint toward a distant radio source in a direction indicated by the
unit vector
s, and
b is the interferometer baseline
vector. The position pointed by the unit vector
so is commonly
referred to as the phase tracking center or phase reference
position:
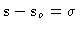 .
.
 |
The object model variable 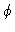 lies in some
object space Ho whose vectors, the functions
lies in some
object space Ho whose vectors, the functions 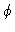 ,
are defined at a high level of resolution. This space
is characterized by two key parameters: the extension
,
are defined at a high level of resolution. This space
is characterized by two key parameters: the extension
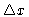 of its field, and its resolution scale
of its field, and its resolution scale 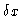 .
To define this object space more explicitly, we first
introduce the finite grid (see Fig. 14.2):
.
To define this object space more explicitly, we first
introduce the finite grid (see Fig. 14.2):
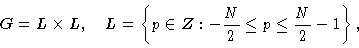 |
(14.1) |
where N is some power of 2.
On each pixel
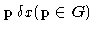 , we
then center a scaling function of the form
, we
then center a scaling function of the form
 |
(14.2) |
Figure:
Object grid
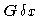 (left hand)
and Fourier grid
(left hand)
and Fourier grid
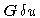 (right hand) for N=8.
The object domain is characterized by its resolution scale
(right hand) for N=8.
The object domain is characterized by its resolution scale 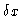 and the extension of its field
and the extension of its field
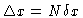 ,
where N is
some power of 2 (the larger is N, the more oversampled is the object
field). The basic Fourier sampling interval is
,
where N is
some power of 2 (the larger is N, the more oversampled is the object
field). The basic Fourier sampling interval is
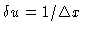 ,
the extension of the Fourier domain is
,
the extension of the Fourier domain is
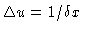 .
.
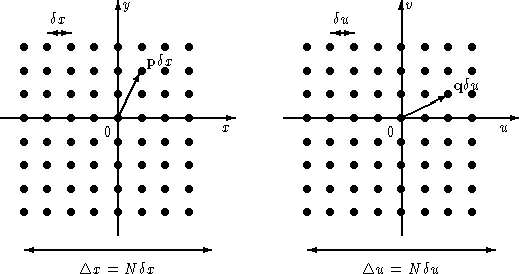 |
It is easy to verify that these functions form an orthogonal set.
In this presentation of WIPE, the object space Hois the Euclidian space generated by the basis vectors
ep,
p spanning
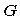 (see Fig. 14.2). The dimension of
this space is equal to N2: the number of pixels in the
grid
(see Fig. 14.2). The dimension of
this space is equal to N2: the number of pixels in the
grid
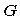 . The functions
. The functions 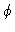 lying in Ho can therefore
be expanded in the form
lying in Ho can therefore
be expanded in the form
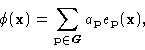 |
(14.3) |
where the
ap's are the components of 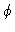 in the
interpolation basis of Ho.
in the
interpolation basis of Ho.
The Fourier transform of 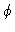 is defined by the relationship
is defined by the relationship
where
u is a two-dimensional angular spatial frequency:
u = (u,v). According to the expansion of 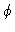 we therefore
have:
we therefore
have:
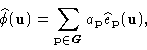 |
(14.4) |
where
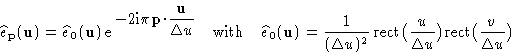 |
(14.5) |
and
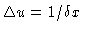 .
.
The dual space of the object space,
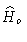 , is the
image of Ho by the Fourier transform operator:
, is the
image of Ho by the Fourier transform operator:
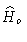 is
the space of the Fourier transforms of the functions
is
the space of the Fourier transforms of the functions 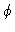 lying
in Ho.
This space is characterized by two key parameters: its
extension
lying
in Ho.
This space is characterized by two key parameters: its
extension
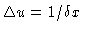 , and the basic Fourier sampling
interval
, and the basic Fourier sampling
interval
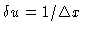 (see Fig. 14.2).
(see Fig. 14.2).



Next: 14.3 Experimental data space
Up: 14. Advanced Imaging Methods:
Previous: 14.1 Introduction
S.Guilloteau
2000-01-19


![]() lies in some
object space Ho whose vectors, the functions
lies in some
object space Ho whose vectors, the functions ![]() ,
are defined at a high level of resolution. This space
is characterized by two key parameters: the extension
,
are defined at a high level of resolution. This space
is characterized by two key parameters: the extension
![]() of its field, and its resolution scale
of its field, and its resolution scale ![]() .
To define this object space more explicitly, we first
introduce the finite grid (see Fig. 14.2):
.
To define this object space more explicitly, we first
introduce the finite grid (see Fig. 14.2):
![]() , we
then center a scaling function of the form
, we
then center a scaling function of the form
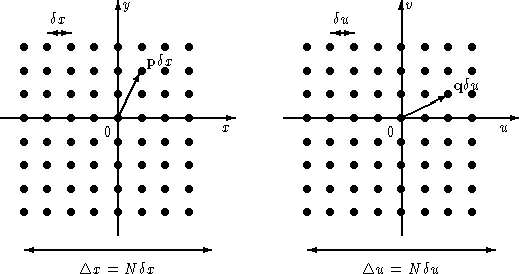
![]() (see Fig. 14.2). The dimension of
this space is equal to N2: the number of pixels in the
grid
(see Fig. 14.2). The dimension of
this space is equal to N2: the number of pixels in the
grid
![]() . The functions
. The functions ![]() lying in Ho can therefore
be expanded in the form
lying in Ho can therefore
be expanded in the form
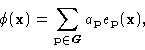
![]() is defined by the relationship
is defined by the relationship
![]() , is the
image of Ho by the Fourier transform operator:
, is the
image of Ho by the Fourier transform operator:
![]() is
the space of the Fourier transforms of the functions
is
the space of the Fourier transforms of the functions ![]() lying
in Ho.
This space is characterized by two key parameters: its
extension
lying
in Ho.
This space is characterized by two key parameters: its
extension
![]() , and the basic Fourier sampling
interval
, and the basic Fourier sampling
interval
![]() (see Fig. 14.2).
(see Fig. 14.2).