


Next: 14.4 Image reconstruction process
Up: 14. Advanced Imaging Methods:
Previous: 14.2 Object space
The experimental data
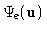 are blurred values
of
are blurred values
of
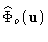 on a finite list of frequencies in the
Fourier domain:
on a finite list of frequencies in the
Fourier domain:
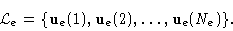 |
(14.6) |
As the object function of interest
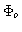 is a
real-valued function, it is natural to define
is a
real-valued function, it is natural to define
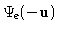 as the complex conjugate of
as the complex conjugate of
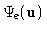 .
The experimental frequency list
.
The experimental frequency list
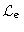 is defined
consequently:
if
is defined
consequently:
if
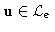 , then
, then
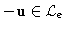 (except for the null frequency
u=: in the convention
adopted here, either it does not lie in
(except for the null frequency
u=: in the convention
adopted here, either it does not lie in
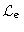 , or there
exists only one occurrence of this point).
The experimental frequency coverage generated by
, or there
exists only one occurrence of this point).
The experimental frequency coverage generated by
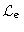 is therefore centrosymmetric (see Fig. 14.3).
is therefore centrosymmetric (see Fig. 14.3).
Figure:
An example of an experimental frequency coverage
provided by the IRAM interferometer. Here, the number of
points Ne in the experimental frequency
list
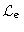 is equal to 2862.
is equal to 2862.
![\resizebox{8.0cm}{!}{\includegraphics[angle=270]{eafig3.eps}}](img1047.gif) |
The experimental data vector
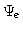 lies in the
experimental data space Ke, the real Euclidian space
underlying the space of complex-valued functions
lies in the
experimental data space Ke, the real Euclidian space
underlying the space of complex-valued functions 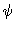 on
on
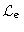 ,
such that
,
such that
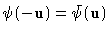 .
The dimension of this space is equal to Ne: the number of points
in the experimental frequency list
.
The dimension of this space is equal to Ne: the number of points
in the experimental frequency list
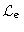 .
.



Next: 14.4 Image reconstruction process
Up: 14. Advanced Imaging Methods:
Previous: 14.2 Object space
S.Guilloteau
2000-01-19
![\resizebox{8.0cm}{!}{\includegraphics[angle=270]{eafig3.eps}}](img1047.gif)
![]() lies in the
experimental data space Ke, the real Euclidian space
underlying the space of complex-valued functions
lies in the
experimental data space Ke, the real Euclidian space
underlying the space of complex-valued functions ![]() on
on
![]() ,
such that
,
such that
![]() .
The dimension of this space is equal to Ne: the number of points
in the experimental frequency list
.
The dimension of this space is equal to Ne: the number of points
in the experimental frequency list
![]() .
.