



Next: 2.6 Array Geometry &
Up: 2. The interferometer principles
Previous: 2.4 Fringe Stopping and
The Complex Visibility is
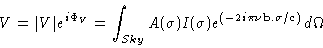 |
(2.31) |
Let (u,v,w) be the coordinate of the baseline vector, in units of the
observing wavelength 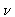 , in a frame of the
phase tracking vector
, in a frame of the
phase tracking vector
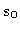 , with w along
, with w along
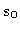 . (x,y,z) are the
coordinates of the source vector
. (x,y,z) are the
coordinates of the source vector
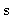 in this frame. Then
in this frame. Then
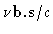 |
= |
ux + vy + wz |
|
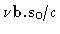 |
= |
w |
|
| z |
= |
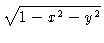 |
|
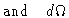 |
= |
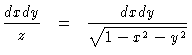 |
(2.32) |
Thus,
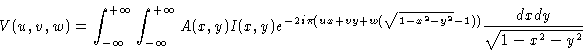 |
(2.33) |
with
I(x,y) = 0 when
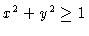 .
.
If (x,y) are sufficiently small, we can make the approximation
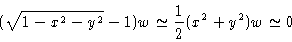 |
(2.34) |
and Eq.2.33 becomes
| V(x,y) |
= |
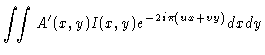 |
(2.35) |
| with A'(x,y) |
= |
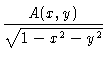 |
(2.36) |
i.e. basically a 2-D Fourier Transform of A I, but
with a phase error term
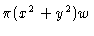 .
Hence, on limited field of views, the relationship between the sky brightness
(multiplied by the antenna power pattern)
and the visibility reduces to a simple 2-D Fourier transform.
.
Hence, on limited field of views, the relationship between the sky brightness
(multiplied by the antenna power pattern)
and the visibility reduces to a simple 2-D Fourier transform.
There are other approximations related to field of view limitations. Let us
quantify these approximations.
- 2-D Fourier Transform
We can further neglect the phase error term in Eq.2.36, if the condition
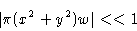 |
(2.37) |
is fulfilled. Now, note that
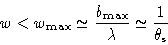 |
(2.38) |
where Beams is the synthesized beam width.
Thus, if
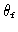 is the field of view to be synthesized, the maximum phase error is
is the field of view to be synthesized, the maximum phase error is
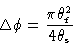 |
(2.39) |
Using
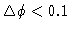 radian (6
radian (6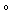 )
as an upper limit (note that this
is the maximum phase error, i.e. the mean phase error is much smaller)
result in the condition (with all angles in radian...):
)
as an upper limit (note that this
is the maximum phase error, i.e. the mean phase error is much smaller)
result in the condition (with all angles in radian...):
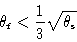 |
(2.40) |
- Bandwidth Smearing
Assume u,v are computed for the center frequency 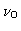 .
At frequency
.
At frequency 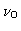 ,
we have
,
we have
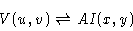 |
(2.41) |
The similarity theorem on Fourier pairs give
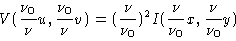 |
(2.42) |
Averaging over the bandwidth
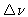 ,
there is a radial smearing
equal to
,
there is a radial smearing
equal to
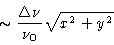 |
(2.43) |
and hence the constraint
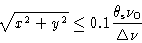 |
(2.44) |
if we want that smearing to be less than 10% of the synthesized beam.
- Time Averaging
Assume for simplicity that the interferometer observes the Celestial Pole.
The baselines cover a sector of
angular width
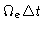 ,
where
,
where 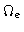 is the Earth rotation
speed, and
is the Earth rotation
speed, and 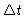 the integration time. The smearing is
circumferential and of magnitude
the integration time. The smearing is
circumferential and of magnitude
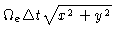 ,
hence the constraint
,
hence the constraint
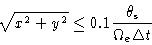 |
(2.45) |
For other declinations, the smearing is no longer rotational, but of similar
magnitude.
To better fix the importance of such approximations, the relevant
values for the Plateau de Bure interferometer are given in Table 2.1.
Table 2.1:
Field of view limitations as function of angular resolution
and observing frequency for the Plateau de Bure interferometer.
| Config. |
Resolution |
Frequency |
2-D |
0.5 GHz |
1 Min Time |
Primary |
| |
|
(GHz) |
Field |
Bandwidth |
Averaging |
Beam |
| Compact |
5'' |
80 GHz |
5' |
80'' |
2' |
60'' |
| Standard |
2'' |
80 GHz |
3.5' |
30'' |
45'' |
60'' |
| Standard |
2'' |
220 GHz |
3.5' |
1.5' |
45'' |
24'' |
| High |
0.5'' |
230 GHz |
1.7' |
22'' |
12'' |
24'' |
|
Note that these fields of view correspond to a maximum phase error of
6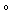 only, or to a (one dimensional) distortion of a tenth of the
synthesized beam, and thus are not strict limits. In particular,
atmospheric errors often results in larger errors (which are
independent of the field of view, however).
only, or to a (one dimensional) distortion of a tenth of the
synthesized beam, and thus are not strict limits. In particular,
atmospheric errors often results in larger errors (which are
independent of the field of view, however).




Next: 2.6 Array Geometry &
Up: 2. The interferometer principles
Previous: 2.4 Fringe Stopping and
S.Guilloteau
2000-01-19