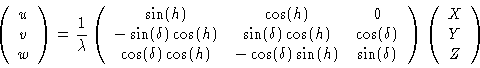2.6 Array Geometry & Baseline Measurements

uv coverage

Using a Cartesian coordinate system (X,Y,Z) with Z towards the pole, X towards the meridian, and Y towards East, the conversion matrix to u,v,w is

$$\left( \begin{array}{c} u \\ v \\ w \end{array} \right) = \fr... ...ight) \left( \begin{array}{c} X \\ Y \\ Z \end{array} \right)$$ (2.46)

where $h , \delta$ are the hour angle and declination of the phase tracking center.

Eliminating h from Eq.2.46 gives the equation of an ellipse:

$$u^2 + \left( \frac{v-(Z/\lambda) \cos(\delta)}{\sin(\delta)} \right)^2 = \frac{X^2+Y^2}{\lambda^2}$$ (2.47)

The uv coverage is an ensemble of such ellipses. The choice of antenna configurations is made to cover the uv plane as much as possible.

Baseline measurement

Assume there is a small baseline error, ( $\Delta X, \Delta Y, \Delta Z$). The phase error is

 

$$\Delta \phi \frac{2 \pi}{\lambda} \Delta \ensuremath{\mathbf b} .\ensuremath{\mathbf s} _0$$ = (2.48)

$$\cos(\delta) \cos(h) \Delta X - \cos(\delta) \sin(h) \Delta Y + \sin(\delta) \Delta Z$$ = (2.49)

Hence, if we observe N sources, we have for each source

$$\phi_k = \phi_0 + \cos(\delta_k) \cos(h_k) \Delta X - \cos(\delta_k) \sin(h_k) \Delta Y + \sin(\delta_k) \Delta Z$$ (2.50)

i.e. a linear system in ( $\Delta X, \Delta Y, \Delta Z$), with N equations and 4 unknown (including the arbitrary phase $\phi_0$). This can be used to determine the baselines from phases measured on a set of sources with known positions $h_k,\delta_k$.

From the shape of Eq.2.49, one can see that the determination of $\Delta X, \Delta Y$ requires large variations in h, preferably at declination $\delta \sim 0$, while that of $\Delta Z$ requires large variations in $\delta$. However, $\phi_k$ in Eq.2.50 is multi-valued (the $2 \pi$ ambiguity...). Hence, the system to solve is in fact

$$mod( \phi_0 + \cos(\delta_k) \cos(h_k) \Delta X - \cos(\delt... ...h_k) \Delta Y + \sin(\delta_k) \Delta Z - \phi_k, 2 \pi) = 0$$ (2.51)

which is a linear system of equations only if $\Delta X, \Delta Y, \Delta Z$are small enough so that the modulo function is the identity. Baseline determination usually proceeds through a ``brute force'' technique, by making a grid search around the most likely values for X,Y,Z.