



Next: 14.5 Implementation of WIPE
Up: 14.4 Image reconstruction process
Previous: 14.4.6 Objective functional
When the problem is well-posed, AE is a one-to-one map
(
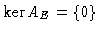 ) from E onto F; the solution is then unique:
there exists only one vector
) from E onto F; the solution is then unique:
there exists only one vector 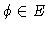 such that
such that
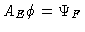 .
This vector,
.
This vector, 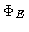 , is said to be the least-squares solution
of the equation
, is said to be the least-squares solution
of the equation 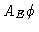 ``=''
``=''
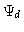 .
.
In this case, let
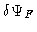 be a variation of
be a variation of 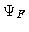 in F,
and
in F,
and
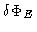 be the corresponding variation of
be the corresponding variation of 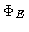 in E(see Fig. 14.7).
It is easy to show that the robustness of the reconstruction process
is governed by the inequality:
in E(see Fig. 14.7).
It is easy to show that the robustness of the reconstruction process
is governed by the inequality:
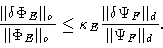 |
(14.17) |
The error amplifier factor 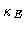 is the condition number of AE:
is the condition number of AE:
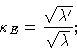 |
(14.18) |
here 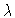 and
and 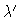 respectively denote the smallest and the
largest eigenvalues of
respectively denote the smallest and the
largest eigenvalues of
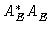 .
The closer to 1 is the condition number, the easier and the more robust
is the reconstruction process (see Fig. 14.8 and 14.9).
.
The closer to 1 is the condition number, the easier and the more robust
is the reconstruction process (see Fig. 14.8 and 14.9).
Figure:
Uniqueness of the solution and robustness of the
reconstruction process. Operator A is an operator from the
object space Ho into the data space Kd.
The object representation space E is a particular
subspace of Ho. The image of E by A, the range of AE,
is denoted by F. In this representation, 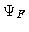 is the
projection of the data vector
is the
projection of the data vector
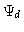 onto F. The inverse problem
must be stated so that AE is a one-to-one map from E onto F,
the condition number
onto F. The inverse problem
must be stated so that AE is a one-to-one map from E onto F,
the condition number 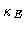 having a reasonable value.
having a reasonable value.
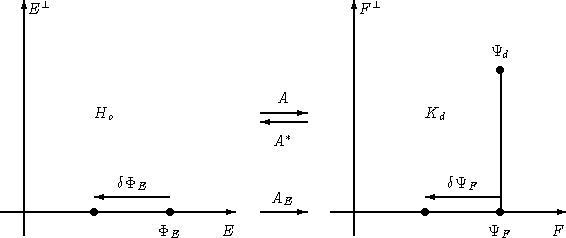 |
The part played by inequality 14.17 in the development of the
corresponding error analysis shows that a good reconstruction
procedure must also provide, in particular, the condition
number 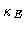 . This is the case of the current implementation
of WIPE which uses the conjugate gradient method
for solving the normal equation 14.16.
. This is the case of the current implementation
of WIPE which uses the conjugate gradient method
for solving the normal equation 14.16.
To conduct the final error analysis, one is led to consider
the eigenvalue decomposition of
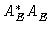 . This is done,
once again, with the aid of the conjugate gradient
method associated with the QR algorithm. At the cost
of some memory overhead (that of the M successive residues), the latter
also yields approximations of the eigenvalues
. This is done,
once again, with the aid of the conjugate gradient
method associated with the QR algorithm. At the cost
of some memory overhead (that of the M successive residues), the latter
also yields approximations of the eigenvalues 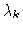 of
of
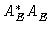 .
It is thus possible to obtain the scalar components of the associated
eigenmodes
.
It is thus possible to obtain the scalar components of the associated
eigenmodes 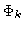 in the interpolation basis of Ho.
The purpose of this analysis is to check whether some of them (in particular
those corresponding to the smallest eigenvalues) are excited or not
in
in the interpolation basis of Ho.
The purpose of this analysis is to check whether some of them (in particular
those corresponding to the smallest eigenvalues) are excited or not
in 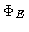 . If so, the corresponding details may be artefacts of the
reconstruction.
. If so, the corresponding details may be artefacts of the
reconstruction.
Figure:
Reconstructed neat map 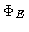 (left hand)
and eigenmode
(left hand)
and eigenmode 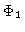 (right hand) corresponding to the
smallest eigenvalue
(right hand) corresponding to the
smallest eigenvalue
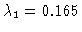 of
of
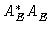 .
The conditions of the simulations are those of Fig. 14.4 and 14.5:
in particular,
the diameter of
.
The conditions of the simulations are those of Fig. 14.4 and 14.5:
in particular,
the diameter of
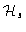 is equal to
is equal to
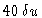 .
The final condition
number is
.
The final condition
number is
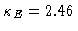 (the eigenvalues of
(the eigenvalues of
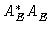 are
plotted on the bar code below). This eigenmode is not excited in
are
plotted on the bar code below). This eigenmode is not excited in  :
the
separation angle
:
the
separation angle 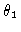 between
between 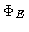 and
and 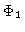 is
greater than
is
greater than 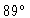 .
In other situations, when the final condition number
is greater, this mode may be at the origin of some artefacts in the
neat map (see Fig. 14.9).
.
In other situations, when the final condition number
is greater, this mode may be at the origin of some artefacts in the
neat map (see Fig. 14.9).
![\begin{picture}(130,59)(0,0)
% width/height=388pt/378pt -> 60mm/59mm
\put(0,0){\...
...> 60mm/59mm
\put(70,0){\includegraphics[width=60mm]{eafig8b.eps} }
\end{picture}](img1103.gif)
![\begin{picture}(120,30)(0,0)
\put(0,18){\resizebox{12.0cm}{!}{\includegraphics[angle=270.0]{eafig8c.eps}} }
\end{picture}](img1104.gif) |
The reconstructed map is then decomposed in the form:
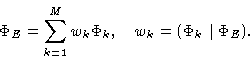 |
(14.19) |
The separation angle 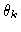 between
between 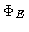 and
and 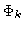 is explicitly given by the relationship:
is explicitly given by the relationship:
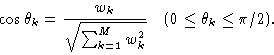 |
(14.20) |
The closer to 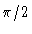 is
is 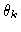 , the less excited is the
corresponding eigenmode
, the less excited is the
corresponding eigenmode 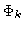 in the reconstructed
neat map
in the reconstructed
neat map 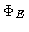 .
.
To illustrate in a concrete manner the interest of equations 14.19 and 14.20,
let us consider the simulations presented in Fig. 14.4 and 14.9.
Whatever the
value of the final condition number is, the error analysis allows the
astronomer to check if there exists a certain similitude between some details
in the neat map and some features of the critical eigenmodes.
This information is very attractive, in particular when the resolution of
the reconstruction process is greater than a reasonable value
(the larger is the aperture to be synthesized
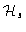 ,
the smaller is the full width at half-maximum of
,
the smaller is the full width at half-maximum of 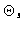 ).
In such situations of ``super resolution,'' the error analysis will
suggest the astronomer to redefined the problem at a lower level of
resolution, or to keep in mind that some details in the reconstructed
neat map may be artefacts of the reconstruction process.
).
In such situations of ``super resolution,'' the error analysis will
suggest the astronomer to redefined the problem at a lower level of
resolution, or to keep in mind that some details in the reconstructed
neat map may be artefacts of the reconstruction process.
Figure:
Reconstructed neat map 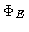 (left hand)
and related critical eigenmode
(left hand)
and related critical eigenmode 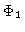 (right hand). The latter
corresponds to the smallest eigenvalue
(right hand). The latter
corresponds to the smallest eigenvalue
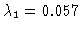 of
of
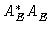 .
The conditions of the simulations are those of Fig. 14.5, but here the diameter
of
.
The conditions of the simulations are those of Fig. 14.5, but here the diameter
of
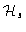 is taken equal to
is taken equal to
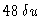 :
the final condition number
is
:
the final condition number
is
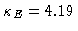 (the eigenvalues of
(the eigenvalues of
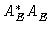 are plotted
on the bar code below). The critical eigenmode
are plotted
on the bar code below). The critical eigenmode 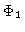 is at the
origin of the oscillations along the main structuring entity of
is at the
origin of the oscillations along the main structuring entity of 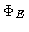 .
This mode is slightly excited (the separation angle
.
This mode is slightly excited (the separation angle 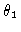 between
between 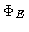 and
and 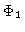 is less than
is less than 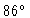 ), thus the
corresponding details may be artefacts. In this case of ``super-resolution''
the error analysis provided by WIPE suggests that the procedure
should be restarted at a lower level of resolution (see Fig. 14.8),
so that the final solution be more stable and reliable.
), thus the
corresponding details may be artefacts. In this case of ``super-resolution''
the error analysis provided by WIPE suggests that the procedure
should be restarted at a lower level of resolution (see Fig. 14.8),
so that the final solution be more stable and reliable.
![\begin{picture}(130,59)(0,0)
% width/height=388pt/378pt -> 60mm/59mm
\put(0,0){\...
...> 60mm/59mm
\put(70,0){\includegraphics[width=60mm]{eafig9b.eps} }
\end{picture}](img1113.gif)
![\begin{picture}(120,30)(0,0)
\put(0,18){\resizebox{12.0cm}{!}{\includegraphics[angle=270.0]{eafig9c.eps}} }
\end{picture}](img1114.gif) |




Next: 14.5 Implementation of WIPE
Up: 14.4 Image reconstruction process
Previous: 14.4.6 Objective functional
S.Guilloteau
2000-01-19
![]() be a variation of
be a variation of ![]() in F,
and
in F,
and
![]() be the corresponding variation of
be the corresponding variation of ![]() in E(see Fig. 14.7).
It is easy to show that the robustness of the reconstruction process
is governed by the inequality:
in E(see Fig. 14.7).
It is easy to show that the robustness of the reconstruction process
is governed by the inequality:
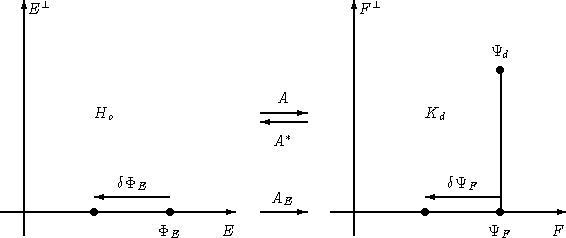
![]() . This is the case of the current implementation
of WIPE which uses the conjugate gradient method
for solving the normal equation 14.16.
. This is the case of the current implementation
of WIPE which uses the conjugate gradient method
for solving the normal equation 14.16.
![]() . This is done,
once again, with the aid of the conjugate gradient
method associated with the QR algorithm. At the cost
of some memory overhead (that of the M successive residues), the latter
also yields approximations of the eigenvalues
. This is done,
once again, with the aid of the conjugate gradient
method associated with the QR algorithm. At the cost
of some memory overhead (that of the M successive residues), the latter
also yields approximations of the eigenvalues ![]() of
of
![]() .
It is thus possible to obtain the scalar components of the associated
eigenmodes
.
It is thus possible to obtain the scalar components of the associated
eigenmodes ![]() in the interpolation basis of Ho.
The purpose of this analysis is to check whether some of them (in particular
those corresponding to the smallest eigenvalues) are excited or not
in
in the interpolation basis of Ho.
The purpose of this analysis is to check whether some of them (in particular
those corresponding to the smallest eigenvalues) are excited or not
in ![]() . If so, the corresponding details may be artefacts of the
reconstruction.
. If so, the corresponding details may be artefacts of the
reconstruction.
![\begin{picture}(130,59)(0,0)
% width/height=388pt/378pt -> 60mm/59mm
\put(0,0){\...
...> 60mm/59mm
\put(70,0){\includegraphics[width=60mm]{eafig8b.eps} }
\end{picture}](img1103.gif)
![\begin{picture}(120,30)(0,0)
\put(0,18){\resizebox{12.0cm}{!}{\includegraphics[angle=270.0]{eafig8c.eps}} }
\end{picture}](img1104.gif)
![]() ,
the smaller is the full width at half-maximum of
,
the smaller is the full width at half-maximum of ![]() ).
In such situations of ``super resolution,'' the error analysis will
suggest the astronomer to redefined the problem at a lower level of
resolution, or to keep in mind that some details in the reconstructed
neat map may be artefacts of the reconstruction process.
).
In such situations of ``super resolution,'' the error analysis will
suggest the astronomer to redefined the problem at a lower level of
resolution, or to keep in mind that some details in the reconstructed
neat map may be artefacts of the reconstruction process.
![\begin{picture}(130,59)(0,0)
% width/height=388pt/378pt -> 60mm/59mm
\put(0,0){\...
...> 60mm/59mm
\put(70,0){\includegraphics[width=60mm]{eafig9b.eps} }
\end{picture}](img1113.gif)
![\begin{picture}(120,30)(0,0)
\put(0,18){\resizebox{12.0cm}{!}{\includegraphics[angle=270.0]{eafig9c.eps}} }
\end{picture}](img1114.gif)