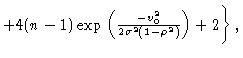Next: 5. LO System and
Up: 4.5 Appendix
Previous: 4.5.1 Summary of definitions
The following determination of the clipping correction is due to
[Hagen et al 1973]:
Given two jointly normal random variables x and y with covariance 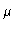 ,
and given some arbitrary function g(x,y), Price's theorem states that
,
and given some arbitrary function g(x,y), Price's theorem states that
 |
(4.24) |
For random signals of zero mean, the covariance  is identical with the
cross-correlation function
is identical with the
cross-correlation function
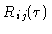 defined in Eq.4.1. As
shown by Eq.4.1, we need to accumulate products of the voltage
outputs of two antennas (i,j), but using the quantized signals rather than
the continuous ones. Thus, with
the identification
x = vi(t) and
defined in Eq.4.1. As
shown by Eq.4.1, we need to accumulate products of the voltage
outputs of two antennas (i,j), but using the quantized signals rather than
the continuous ones. Thus, with
the identification
x = vi(t) and
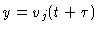 , and using
, and using 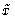 and
and 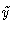 for the quantized signals, we can apply Price's theorem to the
4-level cross-correlation function
for the quantized signals, we can apply Price's theorem to the
4-level cross-correlation function
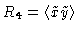 such that
such that
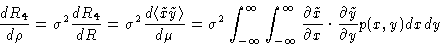 |
(4.25) |
(
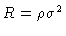 denotes the continuous cross correlation function,
for the sake of simplicity, antenna indices are omitted). The partial
derivatives in the integrand are easily found by using the transfer function
shown in Fig.4.5:
denotes the continuous cross correlation function,
for the sake of simplicity, antenna indices are omitted). The partial
derivatives in the integrand are easily found by using the transfer function
shown in Fig.4.5:
![\begin{displaymath}\tilde{x} = \Theta(x)+(n-1)\left[\Theta(x-v_0)-\Theta(-x-v_0)
\right] \Theta(-x)
\end{displaymath}](img469.gif) |
(4.26) |
where
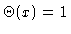 for x>0, and 0 else. Thus,
for x>0, and 0 else. Thus,
![\begin{displaymath}\frac{\partial \tilde{x}}{\partial x} = 2\delta(x)+(n-1)\left[
\delta(x-v_0)+\delta(x+v_0)\right]
\end{displaymath}](img471.gif) |
(4.27) |
Re-writing Price's theorem, we find
Inserting the jointly normal distribution p(x,y), and evaluating the
integral yields
or, alternatively, the integral form given in Eq.4.11.




Next: 5. LO System and
Up: 4.5 Appendix
Previous: 4.5.1 Summary of definitions
S.Guilloteau
2000-01-19
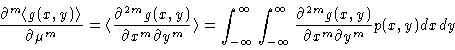
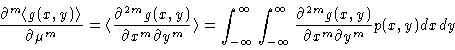
![$\displaystyle \sigma^2 \int_{-\infty}^{\infty}
{\int_{-\infty}^{\infty}{
\left(2\delta(x)+(n-1)\left[\delta(x-v_0)+\delta(x+v_0)\right]
\right)}}$](img473.gif)
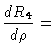
![$\textstyle \frac{\sigma^2}{\pi}
\frac{1}{\sqrt{1-r^2}}\biggl\{(n-1)^2
\left[\ex...
...a^2(1+\rho)}\right)}+
\exp{\left(\frac{-v_0^2}{\sigma^2(1-\rho)}\right)}\right]$](img476.gif)