Many quantization schemes exist (see e.g. [Cooper 1970]). It is entirely
sufficient to use merely a few quantum steps, if the cross-correlation
function will be later corrected for the effects of quantization. For the sake
of illustration, the transfer function of a four-level 2-bit quantization is
shown in Fig.4.5. Each of the four steps is assigned a sign
bit, and a magnitude bit. After discretizing the signal, the samples from one
antenna are shifted in time, in order to compensate the geometric delay
![]() . The correlator now proceeds in the following way: for each
delay step
. The correlator now proceeds in the following way: for each
delay step ![]() , the
corresponding sign and magnitude bits are put into two registers (one for the
first antenna, and one for the second). The second register is successively
shifted by one sample. In this way, sample pairs from both antennas, separated
by a successively longer time lag, are created. These pairs are multiplied,
using a multiplication table. For the case of four-level quantization, it is
shown in Fig.4.5. Products which are assigned a value of
, the
corresponding sign and magnitude bits are put into two registers (one for the
first antenna, and one for the second). The second register is successively
shifted by one sample. In this way, sample pairs from both antennas, separated
by a successively longer time lag, are created. These pairs are multiplied,
using a multiplication table. For the case of four-level quantization, it is
shown in Fig.4.5. Products which are assigned a value of
![]() are called ``high-level products'', those with a value of
are called ``high-level products'', those with a value of ![]() are ``intermediate-level products'', and those with a value of
are ``intermediate-level products'', and those with a value of ![]() ``low-level products''.
The products (evaluated using the multiplication table in
Fig.4.5) are
send to a counter (one counter for each channel,
i.e. for each of the discrete time lags). After the end of the integration
cycle, the counters are read out.
``low-level products''.
The products (evaluated using the multiplication table in
Fig.4.5) are
send to a counter (one counter for each channel,
i.e. for each of the discrete time lags). After the end of the integration
cycle, the counters are read out.
In practice, the multiplication table will be shifted by a positive offset of n2, to avoid negative products (the offset needs to be corrected when the counters are read out). This is because the counter is simply an adding device. As another simplification, low-level products may be deleted. This makes digital implementation easier, and accounts for a loss of sensitivity of merely 1% (see Table 4.1). Finally, not all bits of the counters' content need to be transmitted (see Section3.3.2).
Before the normalized contents of the counters are Fourier-transformed, they need to be corrected, because the cross-correlation function of quantized data does not equal the cross-correlation function of continuous data. This ``clipping correction'' can be derived using two different methods. As an example for the case of full 4-level quantization:
![\begin{displaymath}N_{01,01} = NP_{01,01} = \frac{N}{2\pi\sigma^2\sqrt{1-\rho^2}...
...[\frac{-(x^2+y^2-2\rho xy)}{2\sigma^2(1-\rho^2)}\right]}dx}dy}
\end{displaymath}](img386.gif) |
(4.9) |
Although the discrete, normalized cross-correlation function and the continuous cross-correlation coefficient are almost linearly dependent within a wide range, the correction is not trivial. An analytical solution is only possible for the case of two-level quantization (``van Vleck correction'' [Van Vleck 1966]).
In practice, several methods are used to numerically implement
Eq.4.11 (in the following, the index k means
k-level quantization). The integrand may be replaced by an interpolating
polynomial, allowing to solve the integral. One may also construct
an interpolating surface
![]() . As already discussed, the
clipping correction cannot recover the loss of sensitivity due to
quantization. The loss of sensitivity for k-level discretization may be
found by evaluating the signal-to-noise ratio
. As already discussed, the
clipping correction cannot recover the loss of sensitivity due to
quantization. The loss of sensitivity for k-level discretization may be
found by evaluating the signal-to-noise ratio
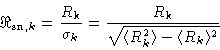 |
(4.11) |
Due to the discretization of the input voltages (as shown in
Fig.4.5), any knowledge of the absolute signal value
is lost. The signal amplitude is recovered by a regularly performed
calibration (using a calibration load of known temperature, for details,
see the lecture by A.Dutrey).
![\resizebox{15.0 cm}{!}{\includegraphics[angle=90.0]{hwfig4.eps}}](img393.gif) |
![\resizebox{15.0 cm}{!}{\includegraphics[angle=270.0]{hwfig5.eps}}](img394.gif) |
| method | n | v0 [
|
|
|
| sampling rate | ||||
|
|
|
|||
| two-level | - | - | 0.64 | 0.74 |
| three-level | - | 0.61 | 0.81 | 0.89 |
| four-level | 3 | 1.00 | 0.88(4) | 0.94 |
| 4 | 0.95 | 0.88 | 0.94 | |
| - | - | 1.00 | 1.00 | |
| Description | Lag window | Spectral window |
| rectangular | w(t) = 1 for
|
|
| Bartlett |
|
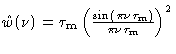 |
| von Hann |
|
|
| Welch |
|
|
| Parzen |
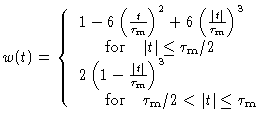
|
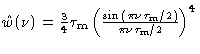 |