



Next: 4.3.1 Digitization of the
Up: 4. Cross Correlators
Previous: 4.2 Basic Theory
In order to numerically evaluate the cross-correlation function
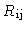 ,
the continuous signals entering the cross correlator need
to be sampled and quantized.
According to Shannon's sampling theorem [Shannon 1949], a
bandwidth-limited signal may be entirely recovered by sampling it at time
intervals
,
the continuous signals entering the cross correlator need
to be sampled and quantized.
According to Shannon's sampling theorem [Shannon 1949], a
bandwidth-limited signal may be entirely recovered by sampling it at time
intervals
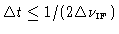 (also called sampling at
Nyquist rate). The discrete Fourier transform of the sufficiently sampled
cross-correlation function theoretically yields the cross-power spectrum
without loss of information. However, in practice, two intrinsic limitations
exist:
(also called sampling at
Nyquist rate). The discrete Fourier transform of the sufficiently sampled
cross-correlation function theoretically yields the cross-power spectrum
without loss of information. However, in practice, two intrinsic limitations
exist:
- In order to discretize a signal, it is not only sampled, it also
has to be quantized. The cross-correlation function, as
derived from quantized signals, does not equal the cross-correlation function
of continuous signals. Moreover, the sampling theorem does not hold anymore for
quantized signals. The reasons will become clear below.
- Eq.4.7 theoretically extends from
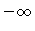 to
to 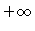 .
In practice (Eq.4.8), only a maximum time lag can be considered: limited storage
capacities and digital processing speed are evident reasons, another limiting
factor are the different timescales mentioned before.
The abrupt cutoff of the time window affects the data.
.
In practice (Eq.4.8), only a maximum time lag can be considered: limited storage
capacities and digital processing speed are evident reasons, another limiting
factor are the different timescales mentioned before.
The abrupt cutoff of the time window affects the data.
These ``intrinsic'' limitations are discussed in Sections 4.3.1 and 4.3.2.
The system-dependent performance will be addressed in Section 4.3.3.




Next: 4.3.1 Digitization of the
Up: 4. Cross Correlators
Previous: 4.2 Basic Theory
S.Guilloteau
2000-01-19