



Next: 4.4 The correlator on
Up: 4.3 The Correlator in
Previous: 4.3.2 Time lag windows
Subsections
4.3.3 Main limitations
In real life, cross-correlators are subject to the performance of the
whole receiving system. This comprises the ``analog part'' (the signal
path from the receivers to the IF filters at the correlator entry),
and the ``digital part'' (everything behind the sampler).
Although the analog part is out of the correlator, its performance
requires to change our assumptions concerning the input data.
This complicates the analysis of the correlator response.
The following discussion refers to instantaneous errors only.
However, in interferometric mapping, scan-averaged visibilities are used,
and the data may be less affected.
The shape of the bandpass function (amplitude and phase) at the correlator
output is mainly due to the correlator's response to the filters inserted in
the IF band at the correlator entry. So far, for the sake of simplicity,
rectangular passbands, centered at the intermediate frequency
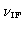 ,
have been assumed. A more complex (and more realistic)
case may be an amplitude slope where the logarithm of the amplitude varies
linearly with frequency. Although the bandpass function will be calibrated
(see Eq.4.17, and R.Lucas chapter 5), the effect of such
a slope on sensitivity remains. A derivation of the signal-to-noise ratio for
that case is beyond the scope of this lecture. To give an impression of the
order of magnitude: a slope of 3.5dB (edge-to-edge) leads to a 2.5%
degradation of the sensitivity calculated for a rectangular passband.
A center frequency displacement of 5% of the bandwidth leads to the same
degradation.
,
have been assumed. A more complex (and more realistic)
case may be an amplitude slope where the logarithm of the amplitude varies
linearly with frequency. Although the bandpass function will be calibrated
(see Eq.4.17, and R.Lucas chapter 5), the effect of such
a slope on sensitivity remains. A derivation of the signal-to-noise ratio for
that case is beyond the scope of this lecture. To give an impression of the
order of magnitude: a slope of 3.5dB (edge-to-edge) leads to a 2.5%
degradation of the sensitivity calculated for a rectangular passband.
A center frequency displacement of 5% of the bandwidth leads to the same
degradation.
As already demonstrated, delay-setting errors linearly increase with
the intermediate frequency
(Eq.4.6). Table4.3 gives an impression of
the decrease of sensitivity due to a delay error. For a range of delay
errors
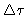 , the effect is also shown in Fig.4.3. For
example, a delay error of
, the effect is also shown in Fig.4.3. For
example, a delay error of
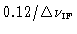 accounts for a
2.5% degradation. Delay errors are mainly due to inaccurately
known antenna positions (asking for better baseline calibration), or
due to errors in the transmission cables.
accounts for a
2.5% degradation. Delay errors are mainly due to inaccurately
known antenna positions (asking for better baseline calibration), or
due to errors in the transmission cables.
Table 4.3:
Effects of delay pattern on the sensitivity
| Intermediate frequency bandwidth |
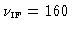 MHz MHz |
| Baseline |
b = 100m |
Zenith distance of source in direction
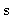 |
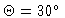 |
| Results in geometric delay: |
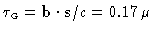 s s |
| Attenuation according to Eq.4.4 |
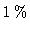 |
Phase errors across the bandpass may also be
of random nature. A phase fluctuation of
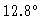 (rms) per scan leads to
a degradation of
(rms) per scan leads to
a degradation of
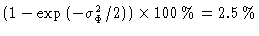 .
.
Figure 4.7:
The Gibbs
phenomenon. The convolution of the bandpass with the (unapodized) spectral window
(sinc function) is shown for the real and imaginary parts. Note that for the real
part, the phenomenon is strongest at the band edges, whereas for the imaginary part,
it contaminates the whole bandpass.
![\resizebox{\hsize}{!}{\includegraphics[angle=270]{hwfig7.eps}}](img428.gif) |
Fluctuations across the bandpass also appear as ripples. They may have
several reasons, and are mainly due to the Gibbs phenomenon,
and due to reflections in the transmission cables. A sinusoidal
bandpass ripple of 2.9dB (peak-to-peak) yields a 2.5% degradation in
the signal-to-noise ratio. The Gibbs phenomenon also occurs in
single-dish autocorrelation spectrometers. For the sake of illustration,
let us again assume a perfectly flat response of receivers and filters.
However, the filter response function is only be flat across the IF passband.
Towards its boundary, steep edges occur. We already learned that strong
spectral lines may show ripples, if no special data windowing in time domain
is applied. The Gibbs phenomen is due to a similar problem (but now the
spectral line is replaced by the edge of a flat rectangular band extending in
frequency from zero to
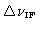 ). The output of the cosine
correlator is symmetric, but the sine output (imaginary part) is
antisymmetric, thus including an even steeper edge. Convolving this edge with
the
). The output of the cosine
correlator is symmetric, but the sine output (imaginary part) is
antisymmetric, thus including an even steeper edge. Convolving this edge with
the
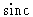 function (i.e. the spectral window) results in strong
oscillations. Let us call this function
function (i.e. the spectral window) results in strong
oscillations. Let us call this function 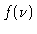 . For calibration purposes,
the Gibbs phenomenon has to be avoided: the problem is that calibration uses
the system response to a flat-spectrum continuum source. A source whose
visibility is
. For calibration purposes,
the Gibbs phenomenon has to be avoided: the problem is that calibration uses
the system response to a flat-spectrum continuum source. A source whose
visibility is 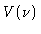 is seen as
is seen as
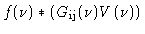 (where
(where
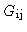 is now a frequency-dependent complex gain function). After
calibration it becomes
is now a frequency-dependent complex gain function). After
calibration it becomes
![\begin{displaymath}\hat{V}(\nu) = \frac{f(\nu)\ast [G_{\rm ij}(\nu)V(\nu)]}{f(\nu)
\ast G_{\rm ij}(\nu)}
\end{displaymath}](img434.gif) |
(4.16) |
You immediately see that the complex gain
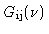 does not
cancel out, as desired, and
does not
cancel out, as desired, and
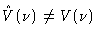 . Automatic calibration
procedures have to flag the channels concerned.
As shown in Fig.4.7, for the cosine correlator, the effect is
strongest at the band edges, but the output of the sine correlator also
shows ripples in the middle of the band (thus, the problem is of greater
importance for interferometers than for single-dish telescopes using
auto-correlators). If the bandwidth to be observed is synthesized by two
adjacent frequency windows, the phenomenon is strongest at the band center
anyhow. You should avoid to place your line there, if it is on top of
an important continuum. To what extent the Plateau de Bure system is concerned, will
be discussed in Section 4.4.1.
. Automatic calibration
procedures have to flag the channels concerned.
As shown in Fig.4.7, for the cosine correlator, the effect is
strongest at the band edges, but the output of the sine correlator also
shows ripples in the middle of the band (thus, the problem is of greater
importance for interferometers than for single-dish telescopes using
auto-correlators). If the bandwidth to be observed is synthesized by two
adjacent frequency windows, the phenomenon is strongest at the band center
anyhow. You should avoid to place your line there, if it is on top of
an important continuum. To what extent the Plateau de Bure system is concerned, will
be discussed in Section 4.4.1.
The above summary of the system-dependent performance of a correlator is not
exhaustive. For example, the phase stability of tunable filters, which depends
on their physical temperature, is not discussed. Alternatives to such filters
are image rejection mixers (as applied in the Plateau de Bure correlator, see
last section).
Errors induced by the digital part are generally negligible with respect
to the analog part. In digital delays, a basic limitation is given by
the discrete nature of the delay compensation, which cannot be more accurate
than given by the clock period of the sampler. However, digital techniques
allow for high clock rates, keeping this error at a minimum.
Evidently, a basic limitation is given by the memory of the counters,
setting the maximum time lag (which in turn defines the spectral resolution,
as already discussed): with 2K bits, we can exactly represent N2Knumbers. However, the information contained in the bits is not equivalent. For
the 3-level correlator, the output of each channel i=1,...,N is
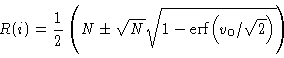 |
(4.17) |
(assuming white, Gaussian noise of zero mean and of unit variance, and
neglecting the weak contribution of the astrophysical signal). The
 -precision of the output is
-precision of the output is
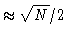 , contained in the
last K-1 bits, which thus do not need to be transmitted. The maximum
integration time before overflow occurs is set by the number of bits of the
counter, and the clock frequency. Table4.4 shows
an example.
, contained in the
last K-1 bits, which thus do not need to be transmitted. The maximum
integration time before overflow occurs is set by the number of bits of the
counter, and the clock frequency. Table4.4 shows
an example.
Table 4.4:
Maximum integration time of a 16-bit counter
| clock frequency: |
80MHz |
| weight for intermediate-level products: |
n = 3 |
| positive offset: |
n2 = 9 |
| weight for autocorrelation product: |
18 (using offset multiplication table) |
| carry out rate of a 4-bit adder |
18/24 = 1.125 |
| maximum integration time: |
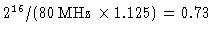 ms ms |
| same with a 4-bit prescaler: |
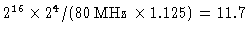 ms ms |
The only error cause due to the correlator that is worth to be mentioned
is the sampler, i.e. the analog-to-digital conversion. As already shown, the
threshold levels are adjusted with respect to the noise in the unquantized
signal. However, the noise power may change during the integration. In that
case, the correlator does not operate anymore at its optimum level (see
Fig.4.4). This error cause can be eliminated with an
automatic level control circuit. However, slight deviations from the
optimal level adjustment may remain. Without going too far into detail,
the deviations can be decomposed in an even and an odd part:
in one case, the positive and negative threshold voltages move into opposed
directions (even part of the threshold error). The resulting error can be
equivalently interpreted as a change of the signal level with respect to the
threshold v0, and leads to a gain error. In the other case, the positive and
negative threshold voltages move into the same direction (odd part of the
threshold error). This error, however, can be reduced by periodic sign
reversal of the digitized samples (if the local oscillator phase is
simultaneously shifted by  , the correlator output remains unaffected).
Combining the original and phase-shifted outputs, the error cancels out with
high precision. Such a phase shift is implemented in the first local
oscillators of the Plateau de Bure system (for details see the lecture by
R.Lucas). Note also that threshold errors of up to 10% can be tolerated
without degrading the correlator sensitivity too much: the examination of
Fig.4.4 shows that such an error results in a
signal-to-noise degradation of less than 0.2% for a 3-level system, and of
less than 0.5% for a 4-level system (the maxima of the efficiency curves
are rather broad).
, the correlator output remains unaffected).
Combining the original and phase-shifted outputs, the error cancels out with
high precision. Such a phase shift is implemented in the first local
oscillators of the Plateau de Bure system (for details see the lecture by
R.Lucas). Note also that threshold errors of up to 10% can be tolerated
without degrading the correlator sensitivity too much: the examination of
Fig.4.4 shows that such an error results in a
signal-to-noise degradation of less than 0.2% for a 3-level system, and of
less than 0.5% for a 4-level system (the maxima of the efficiency curves
are rather broad).
Another problem is that the nominal and actual threshold values may differ.
The error can be described by ``indecision regions''. By calculating the
probability that one or both signals of the cross-correlation product
fall into such an indecision region, the error can be estimated. With
an indecision region of 10% of the nominal threshold value, the
error is negligibly small.
Finally, it should be noted that strict synchronisation between the
cosine and the sine correlators is needed. Any deviation will introduce
a phase error.




Next: 4.4 The correlator on
Up: 4.3 The Correlator in
Previous: 4.3.2 Time lag windows
S.Guilloteau
2000-01-19
![]() , the effect is also shown in Fig.4.3. For
example, a delay error of
, the effect is also shown in Fig.4.3. For
example, a delay error of
![]() accounts for a
2.5% degradation. Delay errors are mainly due to inaccurately
known antenna positions (asking for better baseline calibration), or
due to errors in the transmission cables.
accounts for a
2.5% degradation. Delay errors are mainly due to inaccurately
known antenna positions (asking for better baseline calibration), or
due to errors in the transmission cables.
![]() (rms) per scan leads to
a degradation of
(rms) per scan leads to
a degradation of
![]() .
.
![\resizebox{\hsize}{!}{\includegraphics[angle=270]{hwfig7.eps}}](img428.gif)
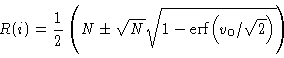
![]() , the correlator output remains unaffected).
Combining the original and phase-shifted outputs, the error cancels out with
high precision. Such a phase shift is implemented in the first local
oscillators of the Plateau de Bure system (for details see the lecture by
R.Lucas). Note also that threshold errors of up to 10% can be tolerated
without degrading the correlator sensitivity too much: the examination of
Fig.4.4 shows that such an error results in a
signal-to-noise degradation of less than 0.2% for a 3-level system, and of
less than 0.5% for a 4-level system (the maxima of the efficiency curves
are rather broad).
, the correlator output remains unaffected).
Combining the original and phase-shifted outputs, the error cancels out with
high precision. Such a phase shift is implemented in the first local
oscillators of the Plateau de Bure system (for details see the lecture by
R.Lucas). Note also that threshold errors of up to 10% can be tolerated
without degrading the correlator sensitivity too much: the examination of
Fig.4.4 shows that such an error results in a
signal-to-noise degradation of less than 0.2% for a 3-level system, and of
less than 0.5% for a 4-level system (the maxima of the efficiency curves
are rather broad).