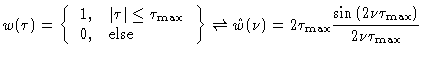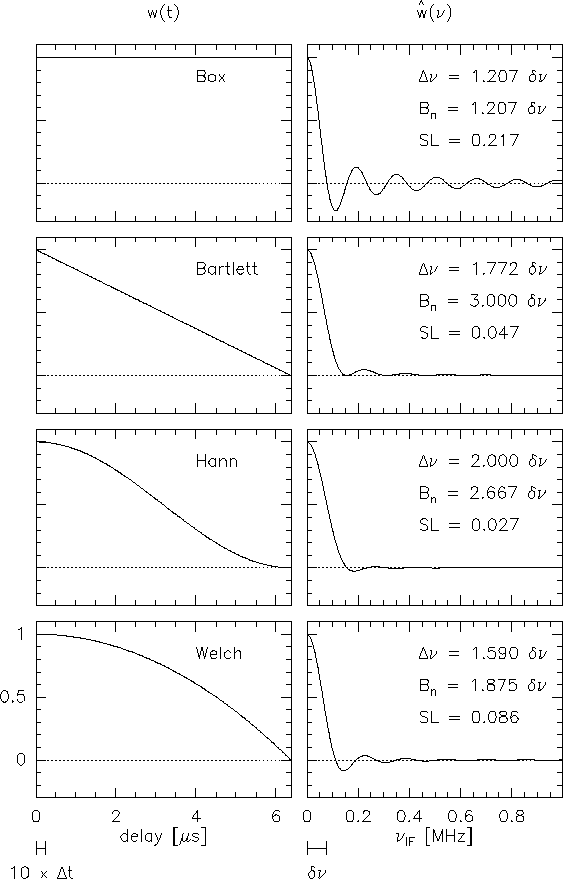Next: 4.3.3 Main limitations
Up: 4.3 The Correlator in
Previous: 4.3.1 Digitization of the
4.3.2 Time lag windows and spectral resolution
According to the sampling theorem, we can recover the cross-power spectral
density within a bandwidth
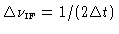 , if the
sampling step is
, if the
sampling step is 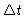 . The channel spacing
. The channel spacing 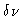 is then
determined by the maximum time lag
is then
determined by the maximum time lag
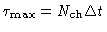 (where
(where
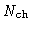 is the number of channels), i.e.
is the number of channels), i.e.
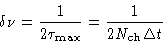 |
(4.13) |
However, the data acquisition is abruptly stopped after the maximum time
lag. After the Fourier transform, the observed cross power spectrum is
convolved with the Fourier transform
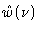 of the box-shaped time
window w(t), producing strong sidelobes:
of the box-shaped time
window w(t), producing strong sidelobes:
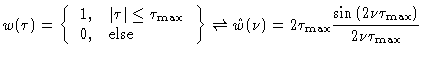 |
|
|
(4.14) |
These oscillations are especially annoying, if strong lines are observed. They
may be minimized, if the box-shaped time lag window is replaced by a function
that rises from zero to peak at negative time lags, and decreases to zero at
positive time lags (apodization). Such a window function suppresses the
sidelobes, at the cost of spectral resolution. A comparison between several
window functions is given in Fig.4.6, together with sidelobe
levels and spectral resolutions (defined by the FWHP of the main lobe
of the spectral window). Table 4.2 summarizes the various
functions in time and spectral domains. The default of the Plateau de Bure
correlator is the Welch window, because it still offers a good spectral
resolution. Moreover, the oscillating sidelobes partly cancel out the
contamination of a channel by the signals in adjacent channels. Of course, the
observer is free to deconvolve the spectra from this default window, and to
use another time lag window.
Note: If you apodize your data, not only the effective spectral
resolution is changed. Due to the suppression of noise at large time lags,
the sensitivity is increased. The variance ratio of apodized data to
unapodized data,
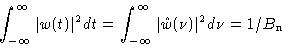 |
(4.15) |
defines the noise equivalent bandwidth 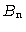 . It is the width of an
ideal rectangular spectral window (i.e.
. It is the width of an
ideal rectangular spectral window (i.e.
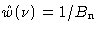 with zero
loss inside
with zero
loss inside
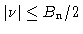 , and infinite loss outside) containing
the same noise power as the actual data. For sensitivity estimates of spectral
line observations, the channel width to be used is thus the noise equivalent
width, and neither the channel spacing, nor the effective spectral resolution.
For commonly used time windows, Fig.4.6 gives the
noise equivalent bandwidths.
, and infinite loss outside) containing
the same noise power as the actual data. For sensitivity estimates of spectral
line observations, the channel width to be used is thus the noise equivalent
width, and neither the channel spacing, nor the effective spectral resolution.
For commonly used time windows, Fig.4.6 gives the
noise equivalent bandwidths.
Figure:
Several time lag
windows, and their Fourier transforms (normalized to peak). The sidelobe levels SL
are indicated, as well as the spectral resolution (defined as the FWHP of the main
lobe), and the noise equivalent width. The delay stepsize, and channel spacing are
indicated for the following example: 256 channels, clock rate 40MHz, resulting in
a channel spacing of 78.125kHz.
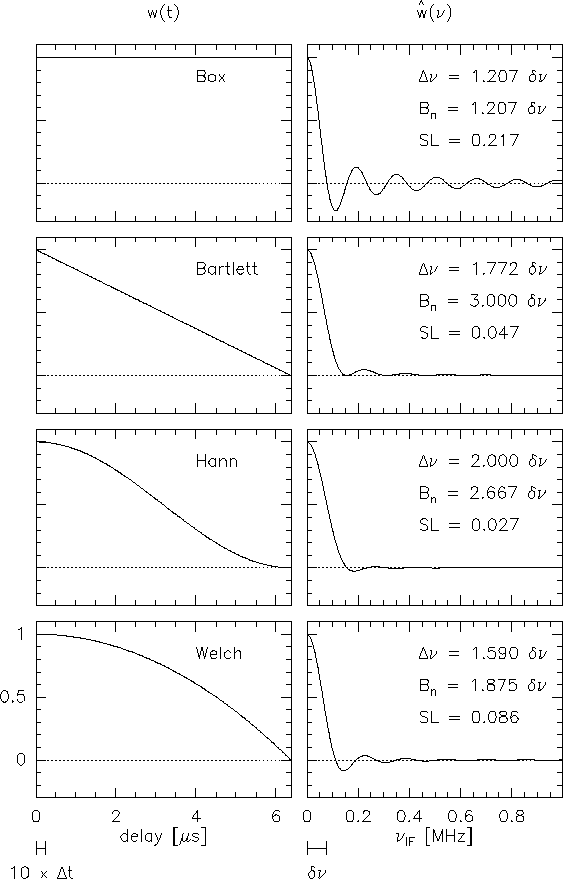 |




Next: 4.3.3 Main limitations
Up: 4.3 The Correlator in
Previous: 4.3.1 Digitization of the
S.Guilloteau
2000-01-19