To actually determine the functions
![]() we observe a strong source,
with a frequency-independent visibility.
The visibilities are
we observe a strong source,
with a frequency-independent visibility.
The visibilities are
| (7.14) |
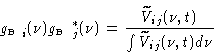 |
(7.15) |
The passband calibrated visibility data will then be:
| (7.16) |
The most important here is the
phase precision: it sets the uncertainty for relative positions of
spectral features in the map. A rule of thumb is:
| (7.17) |
The amplitude accuracy can be very important too, for instance when
one wants to measure a weak line in front of a strong continuum, in
particular for a broad line. In that case one needs to measure the
passband with an amplitude accuracy better than that is needed on
source to get desired signal to noise ratio. Example: we want to
measure a line which is ![]() of the continuum, with a SNR of 20 on
the line strength; then the SNR on the continuum source should be
200, and the SNR on the passband calibration should be at least as
good.
of the continuum, with a SNR of 20 on
the line strength; then the SNR on the continuum source should be
200, and the SNR on the passband calibration should be at least as
good.