


Next: 8.5.3 General case
Up: 8.5 Correction for atmospheric TA*
Previous: 8.5.1 Simplest case
Typically, the mean atmosphere temperature is lower than the ambient temperature
near the ground by about 40 K:
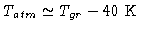 ; then, the
formula above still holds if we replace Tcal by:
; then, the
formula above still holds if we replace Tcal by:
| Tcal |
= |
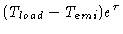 |
(8.33) |
| with Temi |
= |
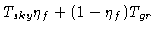 |
|
| |
= |
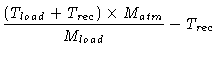 |
(8.34) |
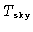 |
= |
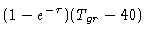 |
|
Trec, the receiver effective temperature is usually calculated by the Yfactor method using a cold load (usually cooled in liquid nitrogen, i.e. at 77 K)
and an ambient load (e.g. at 290 K).
| Y |
= |
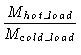 |
|
| Trec |
= |
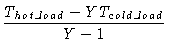 |
(8.35) |



Next: 8.5.3 General case
Up: 8.5 Correction for atmospheric TA*
Previous: 8.5.1 Simplest case
S.Guilloteau
2000-01-19
![]() ; then, the
formula above still holds if we replace Tcal by:
; then, the
formula above still holds if we replace Tcal by: