



Next: 16.3 Experimental data space
Up: 16. Advanced Imaging Methods:
Previous: 16.1 Introduction
Contents
In the problems of Fourier synthesis encountered in astronomy,
the object function of interest,
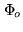 , is a
real-valued function of an angular position variable
, is a
real-valued function of an angular position variable
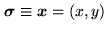 . The geometrical elements
under consideration are presented in Fig. 16.1.
. The geometrical elements
under consideration are presented in Fig. 16.1.
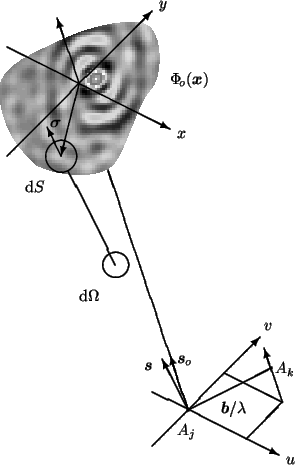
Figure 16.1:
Traditional coordinate systems used to express the
relation between the complex visibilities and the brightness distribution
of a source under observation. Here, the two antennas 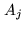 and
and 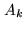 point toward a distant radio source in a direction indicated by the
unit vector
point toward a distant radio source in a direction indicated by the
unit vector
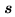 , and
, and
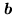 is the interferometer baseline
vector. The position pointed by the unit vector
is the interferometer baseline
vector. The position pointed by the unit vector
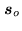 is commonly
referred to as the phase tracking center or phase reference
position:
is commonly
referred to as the phase tracking center or phase reference
position:
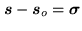 .
.
 |
The object model variable 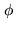 lies in some
object space
lies in some
object space 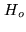 whose vectors, the functions
whose vectors, the functions 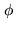 ,
are defined at a high level of resolution. This space
is characterized by two key parameters: the extension
,
are defined at a high level of resolution. This space
is characterized by two key parameters: the extension
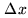 of its field, and its resolution scale
of its field, and its resolution scale 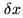 .
To define this object space more explicitly, we first
introduce the finite grid (see Fig. 16.2):
.
To define this object space more explicitly, we first
introduce the finite grid (see Fig. 16.2):
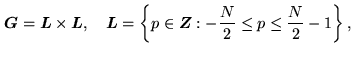 |
(16.1) |
where 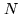 is some power of
is some power of 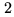 .
.
On each pixel
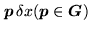 , we
then center a scaling function of the form
, we
then center a scaling function of the form
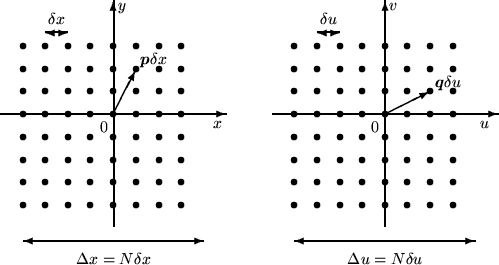
Figure:
Object grid
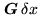 (left hand)
and Fourier grid
(left hand)
and Fourier grid
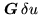 (right hand) for
(right hand) for 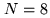 .
The object domain is characterized by its resolution scale
.
The object domain is characterized by its resolution scale 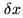 and the extension of its field
and the extension of its field
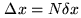 , where
, where 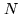 is
some power of
is
some power of 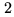 (the larger is
(the larger is 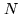 , the more oversampled is the object
field). The basic Fourier sampling interval is
, the more oversampled is the object
field). The basic Fourier sampling interval is
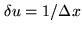 ,
the extension of the Fourier domain is
,
the extension of the Fourier domain is
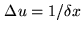 .
.
 |
It is easy to verify that these functions form an orthogonal set.
In this presentation of WIPE, the object space 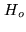 is the Euclidian space generated by the basis vectors
is the Euclidian space generated by the basis vectors
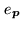 ,
,
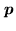 spanning
spanning
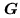 (see Fig. 16.2). The dimension of
this space is equal to
(see Fig. 16.2). The dimension of
this space is equal to 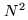 : the number of pixels in the
grid
: the number of pixels in the
grid
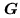 . The functions
. The functions 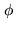 lying in
lying in 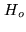 can therefore
be expanded in the form
can therefore
be expanded in the form
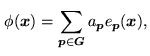 |
(16.3) |
where the
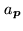 's are the components of
's are the components of 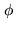 in the
interpolation basis of
in the
interpolation basis of 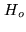 .
.
The Fourier transform of 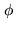 is defined by the relationship
is defined by the relationship
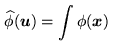 e e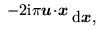 |
|
where
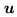 is a two-dimensional angular spatial frequency:
is a two-dimensional angular spatial frequency:
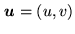 . According to the expansion of
. According to the expansion of 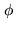 we therefore
have:
we therefore
have:
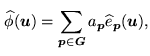 |
(16.4) |
where
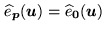 e e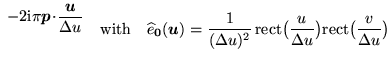 |
(16.5) |
and
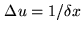 .
.
The dual space of the object space,
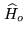 , is the
image of
, is the
image of 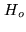 by the Fourier transform operator:
by the Fourier transform operator:
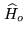 is
the space of the Fourier transforms of the functions
is
the space of the Fourier transforms of the functions 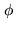 lying
in
lying
in 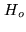 .
This space is characterized by two key parameters: its
extension
.
This space is characterized by two key parameters: its
extension
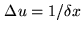 , and the basic Fourier sampling
interval
, and the basic Fourier sampling
interval
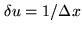 (see Fig. 16.2).
(see Fig. 16.2).




Next: 16.3 Experimental data space
Up: 16. Advanced Imaging Methods:
Previous: 16.1 Introduction
Contents
Anne Dutrey


![]() lies in some
object space
lies in some
object space ![]() whose vectors, the functions
whose vectors, the functions ![]() ,
are defined at a high level of resolution. This space
is characterized by two key parameters: the extension
,
are defined at a high level of resolution. This space
is characterized by two key parameters: the extension
![]() of its field, and its resolution scale
of its field, and its resolution scale ![]() .
To define this object space more explicitly, we first
introduce the finite grid (see Fig. 16.2):
.
To define this object space more explicitly, we first
introduce the finite grid (see Fig. 16.2):
![]() , we
then center a scaling function of the form
, we
then center a scaling function of the form

![]() is the Euclidian space generated by the basis vectors
is the Euclidian space generated by the basis vectors
![]() ,
,
![]() spanning
spanning
![]() (see Fig. 16.2). The dimension of
this space is equal to
(see Fig. 16.2). The dimension of
this space is equal to ![]() : the number of pixels in the
grid
: the number of pixels in the
grid
![]() . The functions
. The functions ![]() lying in
lying in ![]() can therefore
be expanded in the form
can therefore
be expanded in the form
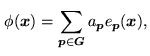
![]() is defined by the relationship
is defined by the relationship
![]() , is the
image of
, is the
image of ![]() by the Fourier transform operator:
by the Fourier transform operator:
![]() is
the space of the Fourier transforms of the functions
is
the space of the Fourier transforms of the functions ![]() lying
in
lying
in ![]() .
This space is characterized by two key parameters: its
extension
.
This space is characterized by two key parameters: its
extension
![]() , and the basic Fourier sampling
interval
, and the basic Fourier sampling
interval
![]() (see Fig. 16.2).
(see Fig. 16.2).