



Next: 16.4 Image reconstruction process
Up: 16. Advanced Imaging Methods:
Previous: 16.2 Object space
Contents
The experimental data
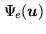 are blurred values
of
are blurred values
of
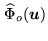 on a finite list of frequencies in the
Fourier domain:
on a finite list of frequencies in the
Fourier domain:
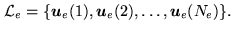 |
(16.6) |
As the object function of interest
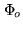 is a
real-valued function, it is natural to define
is a
real-valued function, it is natural to define
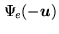 as the complex conjugate of
as the complex conjugate of
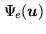 .
The experimental frequency list
.
The experimental frequency list
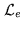 is defined
consequently:
if
is defined
consequently:
if
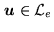 , then
, then
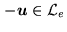 (except for the null frequency
(except for the null frequency
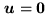 : in the convention
adopted here, either it does not lie in
: in the convention
adopted here, either it does not lie in
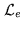 , or there
exists only one occurrence of this point).
The experimental frequency coverage generated by
, or there
exists only one occurrence of this point).
The experimental frequency coverage generated by
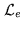 is therefore centrosymmetric (see Fig. 16.3).
is therefore centrosymmetric (see Fig. 16.3).
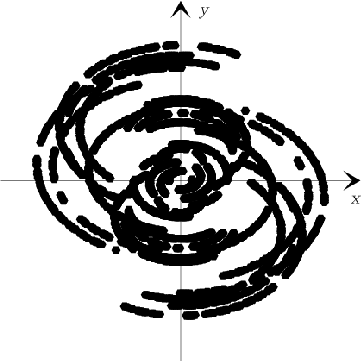
Figure 16.3:
An example of an experimental frequency coverage
provided by the IRAM interferometer. Here, the number of
points 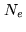 in the experimental frequency
list
in the experimental frequency
list
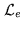 is equal to
is equal to 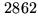 .
.
 |
The experimental data vector
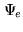 lies in the
experimental data space
lies in the
experimental data space 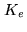 , the real Euclidian space
underlying the space of complex-valued functions
, the real Euclidian space
underlying the space of complex-valued functions 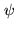 on
on
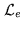 ,
such that
,
such that
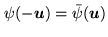 .
The dimension of this space is equal to
.
The dimension of this space is equal to 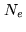 : the number of points
in the experimental frequency list
: the number of points
in the experimental frequency list
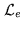 .
.




Next: 16.4 Image reconstruction process
Up: 16. Advanced Imaging Methods:
Previous: 16.2 Object space
Contents
Anne Dutrey

![]() lies in the
experimental data space
lies in the
experimental data space ![]() , the real Euclidian space
underlying the space of complex-valued functions
, the real Euclidian space
underlying the space of complex-valued functions ![]() on
on
![]() ,
such that
,
such that
![]() .
The dimension of this space is equal to
.
The dimension of this space is equal to ![]() : the number of points
in the experimental frequency list
: the number of points
in the experimental frequency list
![]() .
.