17.5 Artifacts and instrumental effects

The behaviour of the mosaicing algorithm towards deconvolution artifacts and/or instrumental effects can be studied by the means of simulations of the whole mosaicing process. The simulations presented below were computed with several models of sky brightness distributions. $uv$-coverages of real observations were used (4-antennas CD configuration of a source of declination $\delta = 68^\circ$). No noise has been added to the simulations shown in the figures, so that pure instrumental effects can directly be seen.

Figure 17.2: Mosaic deconvolved with the CLARK or SDI algorithms. Deconvolution parameters were identical (with a loop gain = 1) and contours are the same in the two images. The formation of stripes does not occur when using the SDI algorithm.

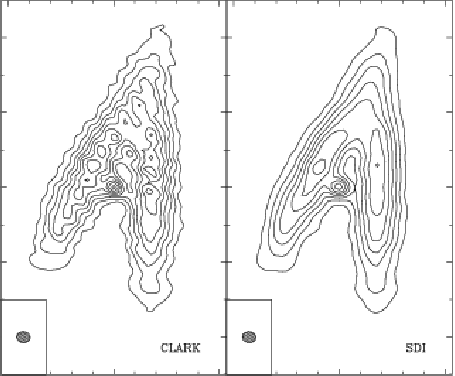Stripes

A well-known instability of the CLEAN algorithm is the formation of stripes during the deconvolution of extended structures. After the dirty beam has been subtracted from the peak of a broad feature, the negative sidelobes of the beam are showing up as positive peaks. The next iterations of the algorithm will then identify these artificial peaks as CLEAN components. A regular separation between the CLEAN components is thereby introduced and the resulting map shows ripples or stripes. [Steer et al. 1984] proposed an enhancement of CLEAN (implemented as the command SDI in MAPPING) which prevents such coherent errors: the CLEAN components are identified and removed in groups. As mosaics are precisely observed to map extended sources, the formation of stripes can a priori be expected. Indeed, the algorithm described in the previous paragraph presents this instability. Fig. 17.2 shows an example of the formation of such ripples. To make them appear so clearly, an unrealistic loop gain ( $\gamma = 1$) was used. Interestingly, the algorithm of [Steer et al. 1984], adapted to the mosaics, does not result in these stripes, even with the same loop gain. It seems thus to be a very efficient solution to get rid of this problem, if it should occur. Note however that more realistic simulations, including noise and deconvolved with normal loop gain, do not show stripes formation. This kind of artifacts seems thus not to play a significant role in the image quality, for the noise and contrast range of typical Plateau de Bure observations. In practice, they are never observed.

Short-spacings

Figure 17.3: Left: Initial model of a very extended sky brightness distribution. Dotted circles indicate the primary beams of the simulated observation. Middle: Reconstructed mosaic, without the short-spacings information. Right: Reconstructed mosaic, with the short-spacings information. The contours are the same in the two simulated observations.

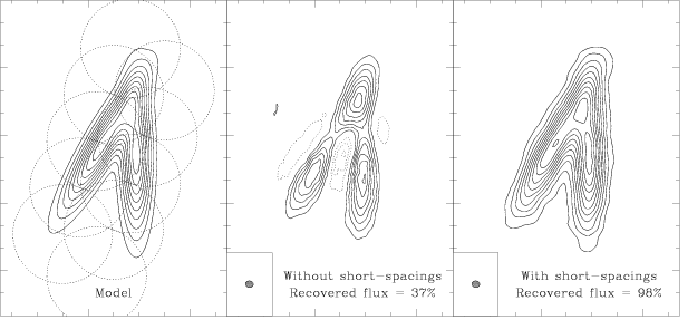The mosaicing technique allows, at least in theory, to recover part of the short-spacings information (see Section 17.2). In practice, however, the lack of the short-spacings cannot be fully compensated, and thus still introduces severe artifacts in the reconstructed images. The mosaic case is actually more complex than the single-field case, because the most extended structures are filtered out in each field, thus introducing a lack of information on an intermediate scale as compared to the size of the mosaic. As a consequence, a very extended emission can be split into several pieces, each one having roughly the size of the primary beam. This effect can be very well seen on the simulation presented in Fig. 17.3. To correct for this problem, it is necessary to add the short-spacings informations (deduced typically from single-dish observations) to the interferometric data set. Note however that the effects of the missing short-spacings on the reconstructed mosaic strongly depend on the actual $uv$-coverage of the observations, as well as on the size and morphology of the source: the artifacts can be small or negligible if the observed emission is confined into reasonably small regions. From this point of view, the example shown in Fig. 17.3 represents the worst case.

In any case, CLEAN is known to be not optimal to deconvolve smooth, extended structures. In order to partially alleviate this problem and the effects of the missing short-spacings, [Wakker & Schwartz 1988] proposed an enhanced algorithm, the so-called multi-resolution CLEAN: deconvolutions are performed at low- and high-resolution, and the results are combined to reconstruct an image which then accounts for the extended structures much better than in the case of a classical CLEAN deconvolution. As already quoted before, this algorithm cannot be applied to a mosaic, because it relies on a linear measurement equation. A multi-resolution CLEAN adapted to mosaics has however been developed ([Gueth 1997]) and is implemented in MAPPING. This method will not be described here.

Figure 17.4: Simulations of a 10-fields mosaic observed with the Plateau de Bure interferometer. Each field is affected by a pointing error (see text). The corresponding rms are indicated in the lower left (observations performed at 115 GHz) and lower right (230 GHz) corners of each panel.

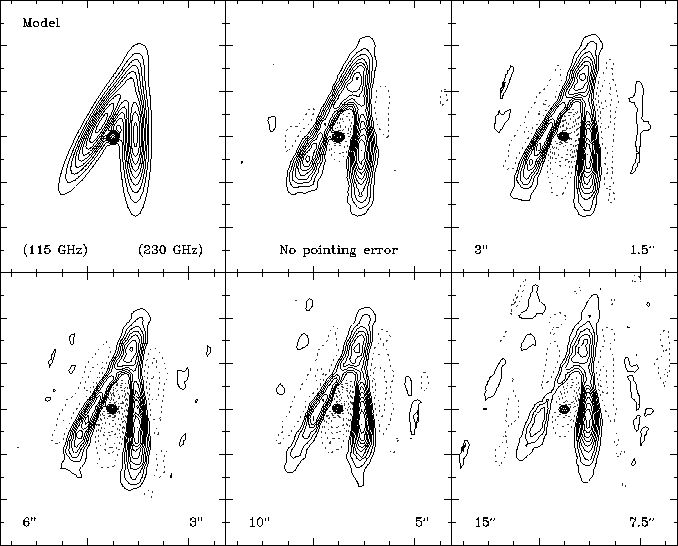Pointing errors

Pointing errors during the observations can of course strongly affect the images obtained by mosaicing. The rms of the pointing errors of the antennas of the Plateau de Bure interferometer is about $3''$. By comparison, the primary beam size at 230 GHz is $\sim$22$''$ (Table 17.1). The pointing errors are difficult to model precisely: they are different for each antenna, random errors as well as slow drifts occur, the amplitude calibration partially corrects them, etc. A complete simulation should therefore introduce pointing errors during the calculation of each visibility. For typical Plateau de Bure observations, such a detailed modeling is probably not necessary, as the final image quality is dominated by deconvolution artifacts. To get a first guess of the influence of pointing errors, less realistic simulations were thus performed, in which each field is shifted as a whole by a (random) quantity. Such a systematic effect most probably maximizes the distortions introduced in the images. (Note that for a single field, the source would simply be observed at a shifted position in such a simulation. For a mosaic, the artifacts are different, because each individual field has a different, random pointing error. See [Cornwell 1987] for a simplified analysis in terms of visibilities. Figure 17.4 presents typical reconstructed mosaics for different rms of the pointing errors of the Plateau de Bure antennas. Obviously, the larger the pointing error, the worse the image quality. With a pointing error rms of $3''$, reasonably correct mosaics can be reconstructed even at 230 GHz. Clearly, care to the pointing accuracy has however to be exercised when mosaicing at the highest frequencies.