



Next: 17.5 Artifacts and instrumental
Up: 17. Mosaicing
Previous: 17.3 Mosaicing in practice
Contents
The dirty mosaic
The dirty maps of each field 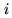 are computed with the same phase
center (i.e. the same coordinate system) and can thus be written:
are computed with the same phase
center (i.e. the same coordinate system) and can thus be written:
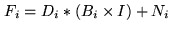 |
(17.10) |
Note that the dirty beams 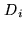 are a priori different for each
pointing center, because the
are a priori different for each
pointing center, because the 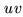 -coverages, even if similar, are
slightly different. The dirty mosaic
-coverages, even if similar, are
slightly different. The dirty mosaic 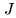 can then be constructed
according to Eq. 17.9:
can then be constructed
according to Eq. 17.9:
![$\displaystyle J = \frac{\displaystyle \sum\nolimits_i \frac{B_i}{\sigma_i^2} ...
...D_i*(B_i\times I)+N_i\Big]}{\displaystyle \sum\nolimits_i B_i^2 \sigma_i^{-2}}$](img1807.png) |
(17.11) |
This relation is homogeneous to the sky brightness distribution 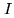 :
the mosaic is corrected for the primary beams attenuation. In
practice, a slightly modified mosaic is computed, in order to avoid
noise propagation (it makes no sense to add to the center of a field
noise coming from the external, attenuated regions of an adjacent
field). For that purpose, the primary beams used to construct the
mosaic are truncated to some value, typically 10 to 30% of the
maximum. The mosaic is thus defined by:
:
the mosaic is corrected for the primary beams attenuation. In
practice, a slightly modified mosaic is computed, in order to avoid
noise propagation (it makes no sense to add to the center of a field
noise coming from the external, attenuated regions of an adjacent
field). For that purpose, the primary beams used to construct the
mosaic are truncated to some value, typically 10 to 30% of the
maximum. The mosaic is thus defined by:
![$\displaystyle J = \frac{\displaystyle \sum\nolimits_i \frac{B_i^t}{\sigma_i^2} ...
...(B_i\times I)+N_i\Big]}{\displaystyle \sum\nolimits_i {B_i^t}^2 \sigma_i^{-2}}$](img1808.png) |
(17.12) |
where 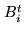 denotes the truncated primary beam of the
field
denotes the truncated primary beam of the
field 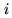 . This relation is the ``measurement equation'' of a mosaic,
connecting the observed quantity
. This relation is the ``measurement equation'' of a mosaic,
connecting the observed quantity 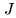 to the sky brightness
distribution
to the sky brightness
distribution 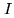 (Eq. 17.1 was the measurement
equation of a single-field observation).
(Eq. 17.1 was the measurement
equation of a single-field observation).
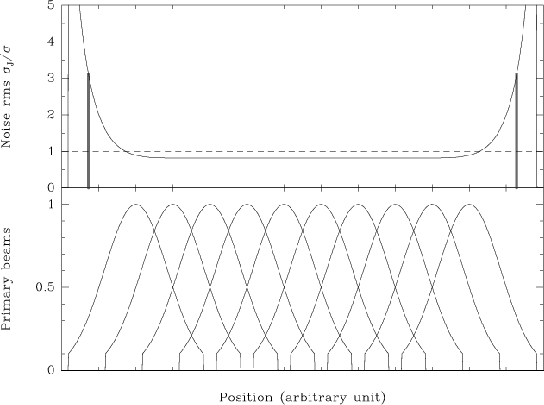
Noise distribution
Figure 17.1:
One-dimensional mosaic of 10 half-power overlapping fields,
with identical noise level 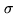 . Lower panel: Normalized primary
beams, truncated to B
. Lower panel: Normalized primary
beams, truncated to B
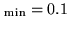 . Upper panel: Resulting noise
distribution (Eq. 17.14). The noise rms in the
mosaic is roughly constant, about 20% lower than the noise of each
individual field, but strongly increases at the edges. The two thick
vertical lines indicate the truncation of the mosaic done by the
algorithm at
. Upper panel: Resulting noise
distribution (Eq. 17.14). The noise rms in the
mosaic is roughly constant, about 20% lower than the noise of each
individual field, but strongly increases at the edges. The two thick
vertical lines indicate the truncation of the mosaic done by the
algorithm at
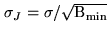 .
.
 |
Due to the correction for the primary beams attenuation, the noise
distribution in a mosaic is not uniform. From Eq. 17.12,
it can be written:
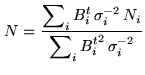 |
(17.13) |
Accordingly, the noise rms 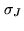 depends on the position and
is given by:
depends on the position and
is given by:
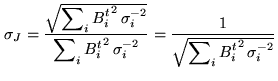 |
(17.14) |
Hence, the noise strongly increases at the edges of the mosaic, and
the resulting image has thus to be truncated (see
Fig. 17.1). The non-uniformity of the noise level with
the position makes it impossible to use classical CLEAN methods to
deconvolve the mosaic: the risk to identify a noise peak as a CLEAN component would be too important. It is thus necessary to identify the
CLEAN components on another distribution. For that purpose, the
``signal-to-noise'' distribution is computed:
Deconvolution algorithm
The main idea of the algorithm is to iteratively find the positions of the CLEAN components on 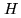 , and then to correct the
mosaic
, and then to correct the
mosaic 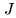 . The initial distributions
. The initial distributions 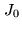 and
and 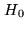 are computed
from the observations and the truncated primary beams, using
Eqs. 17.12 and 17.15. The following
operations have then to be performed at each iteration
are computed
from the observations and the truncated primary beams, using
Eqs. 17.12 and 17.15. The following
operations have then to be performed at each iteration 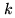 :
:
- Find the position
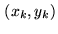 of the maximum of
of the maximum of 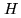 .
.
- Find the value
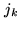 of
of 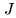 at the position
at the position 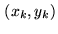 , whether it
is the maximum of
, whether it
is the maximum of 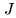 or not.
or not.
- Remove from
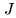 the contribution of a point-like source of intensity
the contribution of a point-like source of intensity
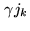 , located at
, located at 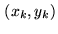 (
(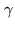 is the loop gain, as in
the normal CLEAN algorithm):
is the loop gain, as in
the normal CLEAN algorithm):
![$\displaystyle J_{k} = J_{k-1} - \frac {\displaystyle\sum\nolimits_i B_i^t \s...
...elta(x_k,y_k)\Big]\Big]}{\displaystyle\sum\nolimits_i {B_i^t}^2 \sigma_i^{-2}}$](img1824.png) |
(17.16) |
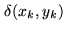 denotes a Dirac peak located at
denotes a Dirac peak located at 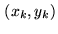 .
.
- Do the same for
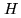 : remove the contribution of a point-like source of
intensity
: remove the contribution of a point-like source of
intensity
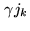 , located at
, located at 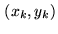 :
:
![$\displaystyle H_k = H_{k-1} - \frac {\displaystyle\sum\nolimits_i B_i^t \sigm...
...,y_k)\Big] \Big]}{\sqrt{\displaystyle\sum\nolimits_i {B_i^t}^2 \sigma_i^{-2}}}$](img1826.png) |
(17.17) |
Note that in the two last relations, the CLEAN component is
multiplied by the true, not truncated, primary beam (taken at the
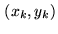 position).
position).
After
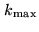 iterations, the mosaic
iterations, the mosaic 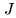 can thus be written:
can thus be written:
![$\displaystyle J = \frac{\displaystyle \sum\nolimits_i B_i^t \sigma_i^{-2} \b...
...bigg]} {\displaystyle \sum\nolimits_i {B_i^t}^2\sigma_i^{-2}} + J_{k_{\rm max}}$](img1828.png) |
(17.18) |
Enough iterations have to be performed to ensure that the residual
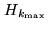 is smaller than some user-specified threshold
(typically 1 to 3). The comparison between Eqs. 17.12 and
17.18 shows that, within the noise, the sum of the
CLEAN components can be identified with the sky brightness
distribution
is smaller than some user-specified threshold
(typically 1 to 3). The comparison between Eqs. 17.12 and
17.18 shows that, within the noise, the sum of the
CLEAN components can be identified with the sky brightness
distribution 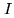 . As with the normal CLEAN algorithm, the final
clean image is then reconstructed as:
. As with the normal CLEAN algorithm, the final
clean image is then reconstructed as:
![$\displaystyle M = C * \left[ \sum_{k=1}^{k_{\rm max}} \gamma j_k \delta(x_k,y_k) \right] + J_{k_{\rm max}}$](img1830.png) |
(17.19) |
where 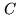 is the chosen clean beam. Note that the algorithm
takes into account the dirty beams being different for each field, but
the restoration is done using a single clean beam, which implicitly
assumes that the dirty beams have similar widths. In practice, the
observing mode of mosaics with the Plateau de Bure interferometer yields similar
is the chosen clean beam. Note that the algorithm
takes into account the dirty beams being different for each field, but
the restoration is done using a single clean beam, which implicitly
assumes that the dirty beams have similar widths. In practice, the
observing mode of mosaics with the Plateau de Bure interferometer yields similar
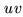 -coverages, and therefore similar dirty beams, for all the fields.
-coverages, and therefore similar dirty beams, for all the fields.
The modified CLEAN algorithms proposed e.g. by [Clark 1980] or
[Steer et al. 1984] can be similarly adapted to handle mosaics, the main
idea being to identify CLEAN components on 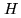 and to correct
and to correct
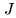 . Note however that the multi-resolution CLEAN [Wakker & Schwartz 1988]
cannot be directly adapted, as it relies on a linear measurement
equation, which is not the case for a mosaic.
. Note however that the multi-resolution CLEAN [Wakker & Schwartz 1988]
cannot be directly adapted, as it relies on a linear measurement
equation, which is not the case for a mosaic.
The MAPPING software
MAPPING is a superset of the GRAPHIC software, which has been
developed to allow more sophisticated deconvolutions to be
performed. For instance, it allows to choose a support for the
deconvolution (clean window) or to monitor the results of the
deconvolution after each iteration. Several enhancements of
CLEAN (e.g. multi-resolution CLEAN) as well as the WIPE
algorithm (see [Lannes et al. 1997]) are also available. The
deconvolution of a mosaic has to be done with MAPPING. The
implemented algorithm assumes that the noise levels in each field
are similar (i.e.
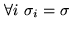 ), which is a
reasonable hypothesis for Plateau de Bure observations. In that case, the
equations of the previous paragraphs are slightly simplified:
), which is a
reasonable hypothesis for Plateau de Bure observations. In that case, the
equations of the previous paragraphs are slightly simplified: 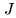 is independent from
is independent from 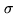 , and
, and 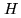 can be written as the ratio
can be written as the ratio
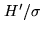 , where
, where 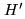 is independent from
is independent from 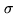 and is used
in practice to localize the CLEAN components.
and is used
in practice to localize the CLEAN components.
We refer to the Mapping Cookbook for a description of the
MAPPING software. To deconvolve mosaics, the following steps are
performed:
- Create a
 table for each observed field.
Then, run the UV_MAP task to compute a dirty map and a dirty
beam for each field, with the same phase center (variable UV_SHIFT = YES).
table for each observed field.
Then, run the UV_MAP task to compute a dirty map and a dirty
beam for each field, with the same phase center (variable UV_SHIFT = YES).
- The task MAKE_MOSAIC is used to combine
the fields to construct a dirty mosaic. Two parameters have to be
supplied: the width and the truncation level
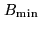 of the
primary beams. Three images are produced: the dirty
mosaic17.3 (yourfile.lmv), all the dirty beams written in the same
file (yourfile.beam), and a file describing the positions and sizes of
the primary beams (yourfile.lobe). The dirty maps and beams of each
individual field are no longer used after this step and can thus be
removed if necessary.
of the
primary beams. Three images are produced: the dirty
mosaic17.3 (yourfile.lmv), all the dirty beams written in the same
file (yourfile.beam), and a file describing the positions and sizes of
the primary beams (yourfile.lobe). The dirty maps and beams of each
individual field are no longer used after this step and can thus be
removed if necessary.
- The data have to be loaded into the MAPPING buffers. This is done by the READ DIRTY yourfile.lmv, READ BEAM yourfile.beam, and READ PRIMARY yourfile.lobe
commands. The latter automatically switches on the mosaic mode of
MAPPING (the prompt is now MOSAIC>). From now, the
deconvolution commands HOGBOM, CLARK and SDI
(for Steer-Dewdney-Ito) can be used and will apply the algorithm
described above. Use the command MOSAIC to switch on or off
the mosaic mode if necessary.
- The clean beam of the final image can be specified
by the user (variables MAJOR and MINOR). Otherwise, the
clean beam computed from the first field is used. To check if there
are differences between the various dirty beams, just use the FIT
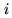 command, which computes the clean beam for the
command, which computes the clean beam for the 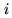 th field.
th field.
- The deconvolution uses the same parameters as a
classical CLEAN: support, loop gain, maximal number of iterations,
maximal value of the final residual, etc.
- In addition, two other parameters, SEARCH_W
and RESTORE_W, can be supplied. Due to the strong increase of
the noise at its edges, the mosaic has to be truncated above some
value of
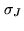 , and these two variables are used to define this
truncation level, in terms of
, and these two variables are used to define this
truncation level, in terms of
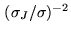 . More
precisely, SEARCH_W indicates the limit above which CLEAN components have not to be searched, while RESTORE_W indicates
the limit above which the clean image is not reconstructed. Default
values of these two parameters (both equal to
. More
precisely, SEARCH_W indicates the limit above which CLEAN components have not to be searched, while RESTORE_W indicates
the limit above which the clean image is not reconstructed. Default
values of these two parameters (both equal to
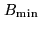 ) are
strongly recommended. The corresponding truncation is shown in
Fig. 17.1.
) are
strongly recommended. The corresponding truncation is shown in
Fig. 17.1.
Tests of the method
Several tests of the method described in this paragraph have been
performed, either with observations (including the comparison of
independent mosaics from the same source) or with simulations. They
show that very satisfactory results can be achieved with typical Plateau de Bure observations. Interestingly, deconvolution of the same data set using
MEM (e.g. the task VTESS in AIPS) seems to give worse
results: this is most probably related to the limited 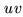 -coverage
obtained with the Plateau de Bure interferometer, as compared to typical VLA observations
(MEM is known to be vulnerable when there is a relatively small
number of visibilities).
-coverage
obtained with the Plateau de Bure interferometer, as compared to typical VLA observations
(MEM is known to be vulnerable when there is a relatively small
number of visibilities).




Next: 17.5 Artifacts and instrumental
Up: 17. Mosaicing
Previous: 17.3 Mosaicing in practice
Contents
Anne Dutrey
![]() are computed with the same phase
center (i.e. the same coordinate system) and can thus be written:
are computed with the same phase
center (i.e. the same coordinate system) and can thus be written:
![$\displaystyle J = \frac{\displaystyle \sum\nolimits_i \frac{B_i}{\sigma_i^2} ...
...D_i*(B_i\times I)+N_i\Big]}{\displaystyle \sum\nolimits_i B_i^2 \sigma_i^{-2}}$](img1807.png)

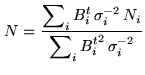
![]() , and then to correct the
mosaic
, and then to correct the
mosaic ![]() . The initial distributions
. The initial distributions ![]() and
and ![]() are computed
from the observations and the truncated primary beams, using
Eqs. 17.12 and 17.15. The following
operations have then to be performed at each iteration
are computed
from the observations and the truncated primary beams, using
Eqs. 17.12 and 17.15. The following
operations have then to be performed at each iteration ![]() :
:
![$\displaystyle J_{k} = J_{k-1} - \frac {\displaystyle\sum\nolimits_i B_i^t \s...
...elta(x_k,y_k)\Big]\Big]}{\displaystyle\sum\nolimits_i {B_i^t}^2 \sigma_i^{-2}}$](img1824.png)
![$\displaystyle H_k = H_{k-1} - \frac {\displaystyle\sum\nolimits_i B_i^t \sigm...
...,y_k)\Big] \Big]}{\sqrt{\displaystyle\sum\nolimits_i {B_i^t}^2 \sigma_i^{-2}}}$](img1826.png)
![]() iterations, the mosaic
iterations, the mosaic ![]() can thus be written:
can thus be written:
![$\displaystyle M = C * \left[ \sum_{k=1}^{k_{\rm max}} \gamma j_k \delta(x_k,y_k) \right] + J_{k_{\rm max}}$](img1830.png)
![]() and to correct
and to correct
![]() . Note however that the multi-resolution CLEAN [Wakker & Schwartz 1988]
cannot be directly adapted, as it relies on a linear measurement
equation, which is not the case for a mosaic.
. Note however that the multi-resolution CLEAN [Wakker & Schwartz 1988]
cannot be directly adapted, as it relies on a linear measurement
equation, which is not the case for a mosaic.
![]() ), which is a
reasonable hypothesis for Plateau de Bure observations. In that case, the
equations of the previous paragraphs are slightly simplified:
), which is a
reasonable hypothesis for Plateau de Bure observations. In that case, the
equations of the previous paragraphs are slightly simplified: ![]() is independent from
is independent from ![]() , and
, and ![]() can be written as the ratio
can be written as the ratio
![]() , where
, where ![]() is independent from
is independent from ![]() and is used
in practice to localize the CLEAN components.
and is used
in practice to localize the CLEAN components.
![]() -coverage
obtained with the Plateau de Bure interferometer, as compared to typical VLA observations
(MEM is known to be vulnerable when there is a relatively small
number of visibilities).
-coverage
obtained with the Plateau de Bure interferometer, as compared to typical VLA observations
(MEM is known to be vulnerable when there is a relatively small
number of visibilities).