- ... output4.1
- The input pupil is the plane where
the electric field coming from the object enters the interferometer.
The output pupil is the plane where the electric field exiting from
each optical train before being combined on the detector.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... theorem)6.1
- Note that the
Fourier transform of a time series is not defined. However, in this context,
we only work with finite sections of a time series.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... filters)6.2
- Because
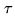 is restricted to a
maximum time lag, this instrumental gain factor does not describe long-term
variations.
is restricted to a
maximum time lag, this instrumental gain factor does not describe long-term
variations.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... correlator6.3
- For the sake of completeness, it should be mentioned that this
is a special case of the so-called Hilbert transform, which property
is to change signal phases by
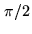 , but to leave amplitudes unchanged.
, but to leave amplitudes unchanged.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... band6.4
- Note that at Bure
the total IF bandwidth available is limited by the receivers to
the range
![$ [100,650]$](img769.png) MHz
MHz
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... distribution17.1
- In the following, we
will assume an uniform noise rms, i.e. we do not take into
account variation of the noise introduced by the imaging process
(see Chapter 15 by S. Guilloteau).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... mapped17.2
- We have considered
observations in different directions, performed with the same
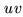 -coverage. The analysis presented here shows that such an
experiment is somehow equivalent to a single observation of the
whole source, but with a denser
-coverage. The analysis presented here shows that such an
experiment is somehow equivalent to a single observation of the
whole source, but with a denser 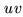 -coverage.
-coverage.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
mosaic17.3
- More precisely, this file contains the non normalized
mosaic
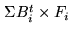 . The proper normalization (see
Eq. 17.12) is further done by the deconvolution
procedures.
. The proper normalization (see
Eq. 17.12) is further done by the deconvolution
procedures.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.