



Next: 4.5 Main challenges in
Up: 4. Introduction to Optical/Near-Infrared
Previous: 4.3 Description of optical
Contents
Subsections
4.4 Formation of the interferometric fringes
In this section, I focus on the light combination and the signal
detection.
4.4.1 Beam combination
[Mariotti et al. 1992] tried to classify the different types of beam
combination (see Fig. 4.7). They have
defined 4 levels of criteria:
- Beam étendue: what is the field accessible by the detector
at each telescope? If this field is limited to the diffraction pattern of
the telescope, then the interferometer is called single-mode,
whereas if the interferometer processes more information than the one in
the diffraction pattern it is multi-mode. For example in radio, all
interferometers are single-mode.
- Beam direction:
Figure 4.8:
All-in-one coaxial (left) and multiaxial (right) 4-way beam
combination schemes.
|
|
how the light coming from the different
arms are combined? If the beams are combined with beam splitters so
that they appear to come from the same direction, then the
combination is called co-axial (see Fig. 4.8a)
and gives a flat tint on the detector. If the beams appear to come
from various direction (see Fig. 4.8b) like in the
Young's experiment the beam combination is called
multi-axial.
- Combination plane:
Figure 4.9:
Combination planes.
|
|
does the beam combination occur in the image plane,
conjugated with the sky, or, in the pupil plane, conjugated
with the telescope pupils (see Fig. 4.9)?
- Relation between the input and output pupils: what is the
interferometric field of view? The answer depends on the relationship
between the input / output4.1 pupil
geometry. One can distinguish 3 cases:
- Fizeau-Stéphan setup where the input and output pupils
are homothetic (both pupil separation and diameters).
- Densified pupil used by the hyper-telescopes [Pedretti et al. 2000]
where the position of the sub-pupils in the output pupil are scaled to
the input ones but the diameters of the sub-pupils are magnified.
- Michelson-Pease setup where there is no link between
the input pupils and the output pupils.
The resulting field of view (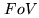 ) are sorted by increasing size:
) are sorted by increasing size:
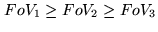 . The Fizeau-Stéphan set-up gives access to a larger
field of view but is difficult to implement since the homethetic relation
must be conserved during the transit of the object. It would require
continuously reconfigurable beam combiners.
. The Fizeau-Stéphan set-up gives access to a larger
field of view but is difficult to implement since the homethetic relation
must be conserved during the transit of the object. It would require
continuously reconfigurable beam combiners.
The tree that corresponds to this classification (see Fig. 4.7) shows the complexity of beam combination in optical
interferometry. However, all but one current interferometers have been
designed to be single-mode, GI2T-REGAIN being the only one using the
multi-mode beam combination scheme.
4.4.2 Fringe coding and detection
Figure 4.10:
Multiaxial beam combination and spatial coding of two-aperture
fringes. Left: the OPD changes with the 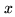 -position on the detector.
Center: the fringes appear superposed to the beam shape. Right:
fringes (
-position on the detector.
Center: the fringes appear superposed to the beam shape. Right:
fringes (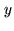 -axis) spectrally dispersed (
-axis) spectrally dispersed (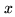 -axis) in the IR channel of
GI2T [Weigelt et al. 2000].
-axis) in the IR channel of
GI2T [Weigelt et al. 2000].
|
|
Figure 4.11:
Coaxial beam combination and temporal coding of two-aperture
fringes. Left: different types of OPD modulation. Center: theoretical
signal. Right: signal observed with the IR table at IOTA.
|
|
Once the beams have been combined, one still needs to detect the fringes.
Since optical detectors have access only to the intensity of the electric
field, the signal must be modulated in phase in order to measure both the
amplitude and the phase of the visibility. The signal measured from the
combination of two arms 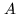 and
and 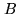 is deduced from Eq. (4.1):
is deduced from Eq. (4.1):
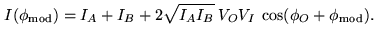 |
(4.4) |
The goal is to evaluate the complex visibility
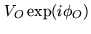 of the object. One needs to modulate
of the object. One needs to modulate
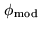 so that the variation of
so that the variation of
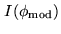 in function of
in function of
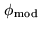 leads to the amplitude of the visibility. There
are mainly two types of fringe coding: the temporal or spatial
coding.
leads to the amplitude of the visibility. There
are mainly two types of fringe coding: the temporal or spatial
coding.
In the multiaxial combination scheme, since the beams from the
different arms come from different directions,
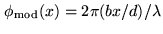 . Therefore analyzing the light at different
positions on the detector plane, gives the visibility information
(see Fig. 4.10). In the coaxial combination
scheme, one introduces a variable optical path length on one arm:
. Therefore analyzing the light at different
positions on the detector plane, gives the visibility information
(see Fig. 4.10). In the coaxial combination
scheme, one introduces a variable optical path length on one arm:
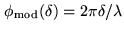 (see Fig. 4.11). There exists also other types of
coding using the polarization or wavelength dependence of the
phase, but they are rarely used.
(see Fig. 4.11). There exists also other types of
coding using the polarization or wavelength dependence of the
phase, but they are rarely used.
When combining more than two beams, one has to decide if one uses
all-in-one or pairwise beam combination. When the number 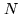 of
telescopes increases the all-in-one combination is prefered
because it involves less optical elements. In a pairwise scheme,
all beams must be splitted in
of
telescopes increases the all-in-one combination is prefered
because it involves less optical elements. In a pairwise scheme,
all beams must be splitted in 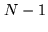 beamlets to be combined with
the other telescopes. The all-in-one solution is displayed both
for co-axial and multi-axial combinations in Fig. 4.8. However, one has to be cautious on the
redundancy of the fringe frequencies so that the signals from two
different baselines are not mixed together. That is why in the
multi-axial combination the sub-pupils are separated by
non-redundant separations, and, in co-axial combination the OPD
scan frequencies and amplitudes are also not redundant.
beamlets to be combined with
the other telescopes. The all-in-one solution is displayed both
for co-axial and multi-axial combinations in Fig. 4.8. However, one has to be cautious on the
redundancy of the fringe frequencies so that the signals from two
different baselines are not mixed together. That is why in the
multi-axial combination the sub-pupils are separated by
non-redundant separations, and, in co-axial combination the OPD
scan frequencies and amplitudes are also not redundant.




Next: 4.5 Main challenges in
Up: 4. Introduction to Optical/Near-Infrared
Previous: 4.3 Description of optical
Contents
Anne Dutrey
![\includegraphics[width=0.9\hsize]{mariotti-bc}](img551.png)
![\includegraphics[width=0.9\hsize]{spatcoding}](img556.png)
![\includegraphics[width=0.9\hsize]{tempcoding}](img557.png)
![]() and
and ![]() is deduced from Eq. (4.1):
is deduced from Eq. (4.1):
![]() . Therefore analyzing the light at different
positions on the detector plane, gives the visibility information
(see Fig. 4.10). In the coaxial combination
scheme, one introduces a variable optical path length on one arm:
. Therefore analyzing the light at different
positions on the detector plane, gives the visibility information
(see Fig. 4.10). In the coaxial combination
scheme, one introduces a variable optical path length on one arm:
![]() (see Fig. 4.11). There exists also other types of
coding using the polarization or wavelength dependence of the
phase, but they are rarely used.
(see Fig. 4.11). There exists also other types of
coding using the polarization or wavelength dependence of the
phase, but they are rarely used.
![]() of
telescopes increases the all-in-one combination is prefered
because it involves less optical elements. In a pairwise scheme,
all beams must be splitted in
of
telescopes increases the all-in-one combination is prefered
because it involves less optical elements. In a pairwise scheme,
all beams must be splitted in ![]() beamlets to be combined with
the other telescopes. The all-in-one solution is displayed both
for co-axial and multi-axial combinations in Fig. 4.8. However, one has to be cautious on the
redundancy of the fringe frequencies so that the signals from two
different baselines are not mixed together. That is why in the
multi-axial combination the sub-pupils are separated by
non-redundant separations, and, in co-axial combination the OPD
scan frequencies and amplitudes are also not redundant.
beamlets to be combined with
the other telescopes. The all-in-one solution is displayed both
for co-axial and multi-axial combinations in Fig. 4.8. However, one has to be cautious on the
redundancy of the fringe frequencies so that the signals from two
different baselines are not mixed together. That is why in the
multi-axial combination the sub-pupils are separated by
non-redundant separations, and, in co-axial combination the OPD
scan frequencies and amplitudes are also not redundant.