



Next: 4.4 Formation of the
Up: 4. Introduction to Optical/Near-Infrared
Previous: 4.2 Optical versus millimeter
Contents
Subsections
4.3 Description of optical interferometers
This section is dedicated to the overview of interferometric systems. We
first go through the functional description of a typical optical
interferometer, then describe the different types of interferometers with
specific objectives.
Optical interferometry aims at measuring the complex degree of coherence of
the observed object. To achieve such a goal, optical interferometers
require the following functionalities:
- Interferometric array. Several types of array configurations
have been designed in order to give access to the different spatial
frequencies (see Fig. 4.2). The three criteria are the
number of telescopes, but also the length and the orientation angle of
their associated baselines. One can choose to have either fixed
telescopes (PTI, KI, VLTI/VIMA) or movable telescopes (GI2T, IOTA,
VLTI/VISA). Like in radio interferometry, Earth rotation allows to sample
the
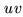 tracks. If the object displays a wavelength-independant
structure like a binary, the coverage of the
tracks. If the object displays a wavelength-independant
structure like a binary, the coverage of the 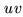 plane can be
performed with spatial frequencies at different wavelengths.
plane can be
performed with spatial frequencies at different wavelengths.
Figure 4.2:
Four examples of optical interferometers. The array can
be linear and continuous (GI2T), L-shaped with several
stations (IOTA), Y-shaped with fixed telescopes (CHARA) or the
filling of an equivalent 200-m aperture (VLTI).
|
|
- Apertures. They ensure the light collection. Either
siderostats (IOTA, PTI, SUSI) with diameter less than
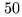 cm or
more or less traditional telescopes (GI2T, CHARA, KI, VLTI) for larger
diameters can be used. In case of large siderostats, a fixed beam
compressor is used to compress the beam diameter for propagation toward
the central lab.
cm or
more or less traditional telescopes (GI2T, CHARA, KI, VLTI) for larger
diameters can be used. In case of large siderostats, a fixed beam
compressor is used to compress the beam diameter for propagation toward
the central lab.
- Beam transportation. Once the object light has been captured
by the apertures, one carries out the individual beams toward the
combination laboratory. Usually the optical path is designed so that a
complete symmetry of the mirrors in each arms minimizes the differential
polarization effects. The optical train contains typically of the order
of 20 mirrors. [Froehly 1981] suggested to use optical fibers to carry
the light from the apertures to the lab. This technology has been tested
by [Coudé Du Foresto, Mazé, & Ridgway 1993] and is the key of the coming O'HANA project which will
gather the light from the 8-m class telescopes on the Maunea Kea in
Hawaii [Perrin et al. 2000]. Some interferometers use vacuum optics (PTI,
IOTA, NPOI,...) to decrease the dispersion due to the propagation in the
air of the delayed beam (see Sect. 4.5.2).
- Wavefront correction. The incoming light travels through the
atmospheric turbulence (see Sect. 4.5.1). The wavefront
is then corrugated and the images of the object move due the
seeing. Almost all interferometers have therefore at least a
2-actuator adaptive optics system that corrects from the tip and the tilt
(IOTA, NPOI, PTI). Large interferometers with aperture diameter larger
than
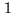 m have plans for higher correction of the wavefront
(VLTI/VIMA, KI-main, GI2T, LBT, CHARA). The goal is to stabilize the
light and to increase the Strehl ratio of individual beams, i.e. the
quality of the central peak. One should note that GI2T currently works in
multi-speckle mode and therefore does not formally require AO systems to
properly work, even if it would increase its sensitivity performance.
m have plans for higher correction of the wavefront
(VLTI/VIMA, KI-main, GI2T, LBT, CHARA). The goal is to stabilize the
light and to increase the Strehl ratio of individual beams, i.e. the
quality of the central peak. One should note that GI2T currently works in
multi-speckle mode and therefore does not formally require AO systems to
properly work, even if it would increase its sensitivity performance.
- Delay lines. When the object observed is traveling across
the sky, the external optical path difference (OPD) between two arms is
equal to
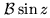 , where
, where 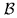 is the baseline length and
is the baseline length and 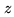 is the
zenith angle. To achieve the fringe detection, the two arms should be
equal at the level of the micrometer. In the first experiment by
[Labeyrie 1975], the stabilization of the OPD was performed by moving the
beam combination table. Nowadays, most interferometers prefer to use
optical delay lines (DL) using cat's eyes located on movable chart.
Moving a DL either in one arm or another compensates the sidereal motion
of the star, exactly like telescope mounts follow the stars
displacements. For very long delays, one often has to design and build
long DLs that offer only optical delays by steps of a few meters coupled
with DLs with shorter strokes (KI, CHARA).
is the
zenith angle. To achieve the fringe detection, the two arms should be
equal at the level of the micrometer. In the first experiment by
[Labeyrie 1975], the stabilization of the OPD was performed by moving the
beam combination table. Nowadays, most interferometers prefer to use
optical delay lines (DL) using cat's eyes located on movable chart.
Moving a DL either in one arm or another compensates the sidereal motion
of the star, exactly like telescope mounts follow the stars
displacements. For very long delays, one often has to design and build
long DLs that offer only optical delays by steps of a few meters coupled
with DLs with shorter strokes (KI, CHARA).
Figure 4.3:
Some examples of delay lines
|
|
- Optical path difference stabilization. The atmospheric
turbulence produces not only wavefront corrugation at the level of
individual apertures but also at the level of the interferometer called
atmospheric piston. The consequence is that the OPD is fluctuating and
the fringes move back and forth. Using a fringe sensor (a simple beam
combiner that measures the OPD at a frequency higher than the typical
atmosphere timescale), one is able to send corrective commands to the
DLs. This feature is the zero-degree of adaptive optics for an
interferometer. A fringe sensor coupled with a DL is called a fringe
tracker and allows to stabilize the signal for longer integration.
- Beam combination.
Figure 4.4:
Beam combiners. Left: beam combiners in bulk optics. Right:
beam combiners using the integrated optics technology.
|
|
The interferences between the various beams can be achieved in many ways
(see Sect. 4.4). One usually distinguishes the so
called co-axial beam combiners (BCs) that combine the light coming from
the same optical axis (like with a beam splitter in the laboratory
Michelson interferometer) and the multi-axial ones that produce
interferences between beams coming from different directions (like in the
Young's experiment). The beam combination is usually made with lenses,
mirrors and/or beam splitters. However, the optical functions used by
the telecommunication industry has given birth to fibered BCs
(e.g. FLUOR [Coudé Du Foresto, Mazé, & Ridgway 1993]) and integrated optics ones (see IONIC
experiment [Malbet et al. 1999]) using single mode waveguides.
- Detection. This fundamental step makes use of photon
detector either with photo-counting capability in the visible range or
CCD with low read-out noise in the infrared. The dispersion of the light
can be done just before the detection and the instrument looks similar to
a spectrograph.
The schematic layout of the VLTI is displayed on Fig. 4.5. It
is typical of most of interferometers. A difference is that the focal plane
hosts several instruments: VINCI the commissioning BC based on
known technology, AMBER the near infrared spectrograph and MIDI the thermal
infrared camera. Smaller interferometers have usually only one dedicated
instrument optimized for their astrophysical targets (binaries, stellar
diameters, envelopes,...).
Figure 4.5:
VLTI optical layout
|
|
4.3.2 Specific applications
I see 5 types of scientific usages of the interferometric light
combination.
Interferometry in the past has been most often used with only two
apertures. Therefore since the atmospheric piston prevents any absolute
phase calibration, the astronomers can only measure the amplitude of the
complex visibility and a phase difference between two spectral channels
when the instrument has some spectroscopic capability. The goal is then to
measure the visibility amplitude or a differential phase, also called
two-color phase, and to interpret the variations of these measurements with
time, with baseline length, or with baseline angle. An important
field of application is the measure of stellar diameters and binary orbits,
but recently it has been extended to circumstellar envelopes and accretion
disks.
The dream of most interferometrists is to perform actual imaging
like in the radio domain using aperture synthesis. The
interferometer COAST has been built with this goal in mind. That
is why it is composed of 4 telescopes in order to increase the
efficiency of the 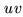 plane coverage, but also to use the
technique of closure phases. This closure phase technique, used to
be of high importance in radio interferometry, allows to
self-calibrate the sum of the phases measured simultaneously by
three baselines. This method is very similar also to the
bispectrum one in speckle interferometry. However for technical
reasons, the beam combination of
plane coverage, but also to use the
technique of closure phases. This closure phase technique, used to
be of high importance in radio interferometry, allows to
self-calibrate the sum of the phases measured simultaneously by
three baselines. This method is very similar also to the
bispectrum one in speckle interferometry. However for technical
reasons, the beam combination of 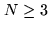 beams appears to be
difficult and only few reconstructed images have been obtained so
far. The outcome of integrated optics might change the situation
in the future [Malbet et al. 1999].
beams appears to be
difficult and only few reconstructed images have been obtained so
far. The outcome of integrated optics might change the situation
in the future [Malbet et al. 1999].
The group working on NPOI has been focusing on the wide-angle
astrometry for a long time (previously at the Mark III interferometer,
ancestor of PTI and NPOI). The idea is simple and once again similar to
what is being done in radio: when the interferometer detects fringes, the
two paths of the interferometer are equal to a fraction of a micrometer.
Since the delay due to the sidereal motion of the stars is given by
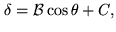 |
(4.2) |
where 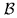 is the length of the baseline,
is the length of the baseline, 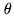 is the
altitude of the star in the sky and
is the
altitude of the star in the sky and 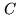 an internal constant, then
the knowledge of
an internal constant, then
the knowledge of 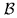 and
and 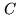 together with the measure of the
stroke given to the DL give access to
together with the measure of the
stroke given to the DL give access to
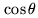 . The objective
consists in measuring the group delay of several tens of stars at
different moments of the night and to fit the curves with cosine
of the same amplitude
. The objective
consists in measuring the group delay of several tens of stars at
different moments of the night and to fit the curves with cosine
of the same amplitude 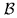 . The internal metrology measures
the internal constant
. The internal metrology measures
the internal constant 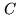 . After post-processing, both the
position of the stars and the baseline are deduced with a
precision of the order of the fringe spacing
. After post-processing, both the
position of the stars and the baseline are deduced with a
precision of the order of the fringe spacing
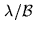 ,
i.e. about 1 mas.
,
i.e. about 1 mas.
Recently, following the work on Mark III, [Shao & Colavita 1992] proposed
the narrow-angle astrometry technique. The idea is to
observe two objects sufficiently close so that the atmospheric
perturbations affecting the stellar path on each telescope is
almost the same for the two objects. The correlations in the
perturbations is used to increase the accuracy of astrometric
measurements down to
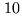
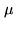 as opening the search for
the reflex motion of stars due to the presence of planets. To
achieve such an objective, one has to separate the field at each
aperture in two sub-apertures and to propagate in parallel the
light from the two stars in two different interferometric systems.
A differential metrology allows to link the two interferometers.
When the fringes are detected on the two detectors, the
differential metrology gives the differential delay between the
two stars:
as opening the search for
the reflex motion of stars due to the presence of planets. To
achieve such an objective, one has to separate the field at each
aperture in two sub-apertures and to propagate in parallel the
light from the two stars in two different interferometric systems.
A differential metrology allows to link the two interferometers.
When the fringes are detected on the two detectors, the
differential metrology gives the differential delay between the
two stars:
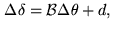 |
(4.3) |
Where
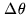 and
and 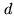 are respectively the differential angle
between the two stars and the internal constant. One interesting
application of such a dual interferometer is phase referencing
like in radio: if a close-by reference star has a zero-phase then the
measure
are respectively the differential angle
between the two stars and the internal constant. One interesting
application of such a dual interferometer is phase referencing
like in radio: if a close-by reference star has a zero-phase then the
measure
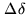 leads to the actual phase of the science target. In
radio, the atmosphere is quiet enough to measure the phase reference by
depointing the interferometer whereas in the optical domain, the two
measurements must be made at the same time. The PTI is the interferometer
that hosts this technique.
leads to the actual phase of the science target. In
radio, the atmosphere is quiet enough to measure the phase reference by
depointing the interferometer whereas in the optical domain, the two
measurements must be made at the same time. The PTI is the interferometer
that hosts this technique.
Finally, many groups are working on the concept of nulling
interferometers. The idea [Bracewell 1978] is to use the coherence of the
light to interferometrically cancel the light arriving in the
interferometer boresight. An object located off-axis has translated
fringes. In certain directions, the bright peaks of the object fringes are
located over the dark zones of the central star fringes. If the nulling in
the dark fringes is high enough, the dynamic range of this technique can
reach high values (see Fig. 4.6).
Figure 4.6:
Principle of a nulling interferometer (see text for details).
|
|
This application is extremely interesting in the case of the study
of extra-solar planets. Those planets are expected to be between
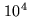 and
and 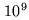 fainter than their parent stars. Nulling the
light of the central star is the only way to detect photons from
these worlds. To achieve such performances, the instruments like
DARWIN pill up several stages of such nulling interferometers to
reach high rejection rate.
fainter than their parent stars. Nulling the
light of the central star is the only way to detect photons from
these worlds. To achieve such performances, the instruments like
DARWIN pill up several stages of such nulling interferometers to
reach high rejection rate.




Next: 4.4 Formation of the
Up: 4. Introduction to Optical/Near-Infrared
Previous: 4.2 Optical versus millimeter
Contents
Anne Dutrey
![\includegraphics[width=0.9\hsize]{bc}](img537.png)
![\includegraphics[width=0.9\hsize]{bc}](img537.png)
![]() plane coverage, but also to use the
technique of closure phases. This closure phase technique, used to
be of high importance in radio interferometry, allows to
self-calibrate the sum of the phases measured simultaneously by
three baselines. This method is very similar also to the
bispectrum one in speckle interferometry. However for technical
reasons, the beam combination of
plane coverage, but also to use the
technique of closure phases. This closure phase technique, used to
be of high importance in radio interferometry, allows to
self-calibrate the sum of the phases measured simultaneously by
three baselines. This method is very similar also to the
bispectrum one in speckle interferometry. However for technical
reasons, the beam combination of ![]() beams appears to be
difficult and only few reconstructed images have been obtained so
far. The outcome of integrated optics might change the situation
in the future [Malbet et al. 1999].
beams appears to be
difficult and only few reconstructed images have been obtained so
far. The outcome of integrated optics might change the situation
in the future [Malbet et al. 1999].
![]()
![]() as opening the search for
the reflex motion of stars due to the presence of planets. To
achieve such an objective, one has to separate the field at each
aperture in two sub-apertures and to propagate in parallel the
light from the two stars in two different interferometric systems.
A differential metrology allows to link the two interferometers.
When the fringes are detected on the two detectors, the
differential metrology gives the differential delay between the
two stars:
as opening the search for
the reflex motion of stars due to the presence of planets. To
achieve such an objective, one has to separate the field at each
aperture in two sub-apertures and to propagate in parallel the
light from the two stars in two different interferometric systems.
A differential metrology allows to link the two interferometers.
When the fringes are detected on the two detectors, the
differential metrology gives the differential delay between the
two stars: