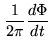Next: 2.2 The Heterodyne Interferometer
Up: 2. Millimetre Interferometers
Previous: 2. Millimetre Interferometers
Contents
The antenna produces a Voltage proportional to
the linear superposition of the incident electric field pattern.
For a simple monochromatic case:
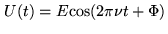 |
(2.1) |
In the receiver, a mixer superimposes the field generated by a
local oscillator to the antenna output.
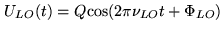 |
(2.2) |
The mixer is a non-linear element (such as a diode) whose output is
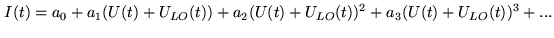 |
(2.3) |
The second order (quadratic) term of Eq.2.3 can be expressed as
Developping the product of the two cosine functions, we obtain
There are obviously other terms in
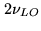 ,
, 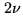 ,
,
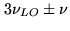 ,
etc...in the above equation, as well as terms at very different frequencies
like
,
etc...in the above equation, as well as terms at very different frequencies
like 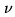 ,
, 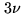 , etc...
, etc...
By inserting a filter at the output of the mixer, we can select only
the term such that
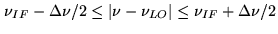 |
(2.6) |
where 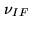 , the so-called Intermediate Frequency, is a frequency
which is significantly different from than the original signal frequency
, the so-called Intermediate Frequency, is a frequency
which is significantly different from than the original signal frequency 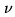 (which is often called the Radio Frequency
(which is often called the Radio Frequency 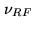 ).
).
Hence, after mixing and filtering, the output of the receiver is
i.e.
- changed in frequency:
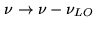 or
or
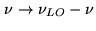
- proportional to the original electric field of the incident wave:
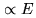
- with a phase relation with this electric field:
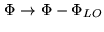 or
or
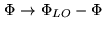
- proportional to the local oscillator voltage:
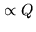
The frequency change, usually towards a lower frequency, allows to
select 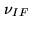 such that amplifiers and transport elements are easily
available for further processing.
The mixer described above accepts simultaneously frequencies which are
(see Fig.2.1)
such that amplifiers and transport elements are easily
available for further processing.
The mixer described above accepts simultaneously frequencies which are
(see Fig.2.1)
- higher than the local oscillator frequency.
This is called Upper Side Band (USB) reception
- lower than the local oscillator frequency.
This is called Lower Side Band (LSB) reception
Figure 2.1:
Relation between the IF, RF and local oscillator frequencies
in an heterodyne system
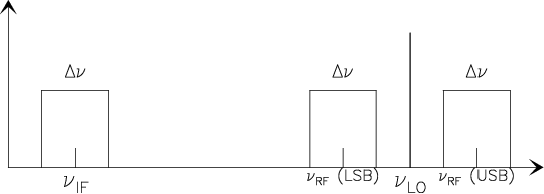 |
and cannot a priori distinguish between them.
This is called Double Side Band (DSB) reception.
Some receivers are actually insensitive
to one of the frequency range, either because a filter has been
placed at the receiver input, or because their response is very strongly
frequency dependent. Such receivers are called Single Side Band (SSB)
receivers.
An important property of the receiving system expressed by
Eq.2.8 is that the sign of the phase is changed for LSB
conversion. This property can be easily retrieved recognizing that the
Frequency 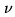 is the time derivative of the Phase
is the time derivative of the Phase 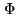 .
Assume the phase varies linearly with time:
.
Assume the phase varies linearly with time:
In this case, the signal
is just another monochromatic signal with slightly shifted frequency.




Next: 2.2 The Heterodyne Interferometer
Up: 2. Millimetre Interferometers
Previous: 2. Millimetre Interferometers
Contents
Anne Dutrey
![]() is the time derivative of the Phase
is the time derivative of the Phase ![]() .
Assume the phase varies linearly with time:
.
Assume the phase varies linearly with time: